International Journal of Civil Infrastructure (IJCI)

ISSN: 2563-8084

1. Introduction

Prestressed concrete has various advantages in comparison to traditional reinforced concrete. Prestressing technique increases the tensile and flexural capacity of the concrete elements in addition to preserving the sustainability concept through the reduction in the usage of materials and sequentially the embodied energy [1-3]. Prestressed concrete elements can be either post- or pre-tensioned: tendons of pre-tensioned elements are stressed before the concrete casting, while in post-tensioned ones, they are stressed after pouring and hardening of concrete. Two types of tendons are used for post-tensioning concrete elements: bonded and unbonded tendons. Bonded tendons (Figure 1) are seven-wires strands inserted inside a plastic or steel duct, and after stressing the strands, grout is injected to fill the duct. Unbonded tendons (Figure 1) are made up of greased seven-wires strands covered with plastic sheathing [2]. Unbonded tendons have many advantages compared to bonded ones such as better corrosion resistance, ease of construction, flexibility and faster construction rate [4].

The major difference between the two types of tendons is the way of stress transfer from the tendon to the concrete, which makes the bonded tendons more widely acceptable in the Egyptian market than the unbonded tendons.

The stress is transferred from the bonded tendon to the concrete via the bond formed due to grouting. Thus, the stress in the tendons can be calculated by the application of the strain compatibility concept. On the other hand, there is no bond between the unbonded tendons and the surrounding concrete due to the presence of the grease and the plastic sheathing [5]. So, empirical equations are adopted by ACI 318-19 [6] provisions to calculate the stress in the unbonded tendons at the ultimate limit state which are given by

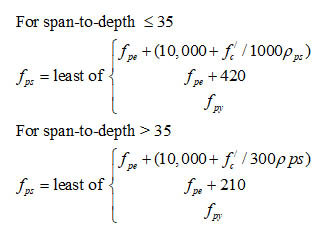
Where, f_ps is the nominal flexural strength of the unbonded tendon, f_pe is the effective prestress of the unbonded tendons, f_py is the yield stress of the tendon, f’_c is the concrete compressive strength, ρ_ps is the ratio of the prestressing tendons cross sectional area to the area of concrete section [A_ps/ bd_p], b is the width of the concrete cross section, and d_p is the effective depth of the prestressing tendons.

There is no provision in this code that requires the usage of non-prestressing bonding reinforcement for the bonded systems but a minimum requirement for bonding reinforcement is required for the unbonded system for crack control. The minimum non-prestressed reinforcement is added to the prestressed members with unbonded tendons to provide a flexural behaviour at the ultimate strength rather than the tied arch behaviour. The provided reinforcement limits the crack width and spacing at the service load state when the tensile stresses acting on the prestressed concrete element surpass the concrete modulus of rupture.

According to the ACI 318-19 [6] provisions the nominal strength allowed for the bonded tendons is higher than the nominal strength allowed for the unbonded tendons. This gap could be supplemented by the usage of non-prestressed reinforcement, so the bonded tendons are not on favour over the unbonded tendons as the price of the supplementary non-prestressed reinforcement is less than the grouting price [6].

2. The Experimental Investigation

2.1. The Slab Specimens

The objective of the current research is to investigate the values of the stress in bonded and unbonded tendons at the ultimate limit state and compare these values for unbonded tendons stress to those resulting from the ACI 318-19 [6] equations. An experimental program is designed to test six one-way post-tensioned slabs with bonded and unbonded tendons monotonically to failure under the effect of four-point flexural loading.

The specimens are chosen of slab type because of the lack of previously carried experimental researches on post-tensioned slab type specimens and due to the wide usage of these slabs in the construction arena. The six specimens are post-tensioned one-way slabs simply supported with span 4.0 meters, width 1.0 meter and thickness 0.16 meters. They are tested under four-point flexural loading. Three sets, each consists of two slabs, are tested. The first set of slabs contains bonded tendons without non-prestressing reinforcement (BS1 and BS2). The second set of slabs contains unbonded tendons without non-prestressing reinforcement (UBS1 and UBS2). The last set of slabs contains unbonded tendons and non-prestressing reinforcement no.10 mm @ 200 mm in the two orthogonal directions according to the ACI 318-19 [6] requirements (UBSR1 and UBSR2). Each slab contains three 12.7 mm diameter seven-wire prestressing strands. The six slabs are designed following the ACI 318-19 [6] provisions with the tendons having double harped profiles and shown in Figure 2. End reinforcement (shown as closed stirrups in Figure 2) is added to the six slabs for resisting stresses produced at the local and general anchorage zones and designed according to the ACI 318-19 [6] provisions. Figure 3 shows the six post-tensioned slab specimens forms with all the reinforcement detailing before concrete casting and after the concrete pouring.

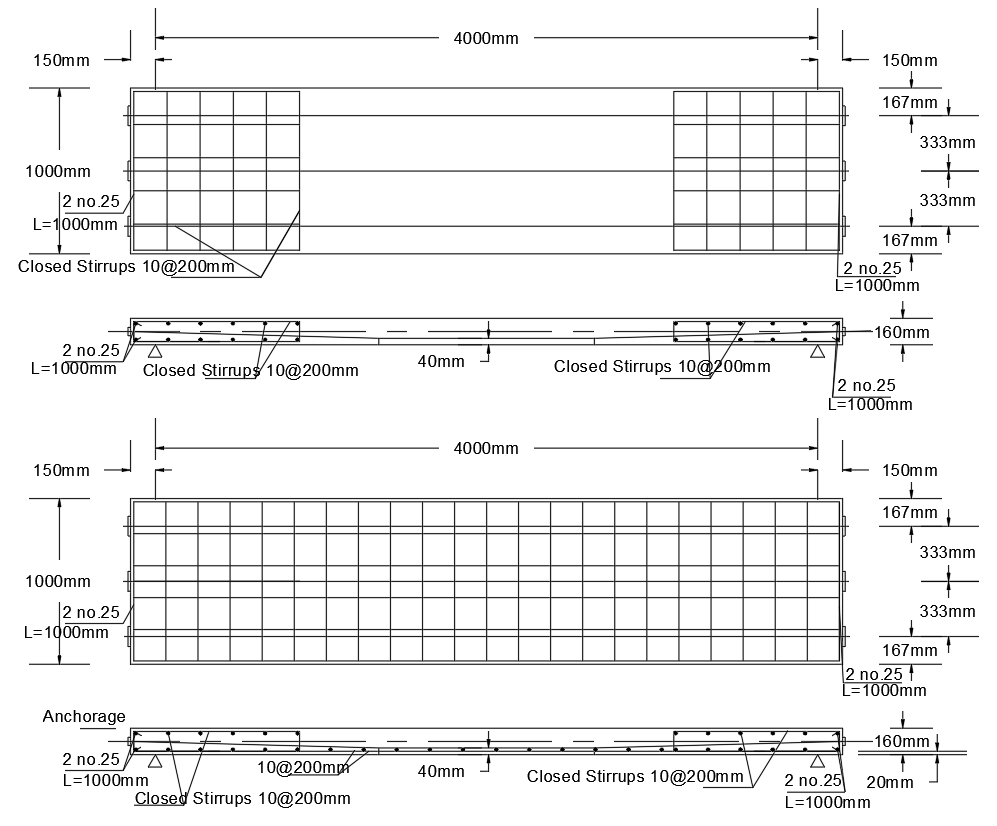
The anchorage system for the bonded slabs is obtained from an Egyptian supplier, Strands-Egypt, while the unbonded anchorage system (Zero void encapsulated system) is imported from GTI-USA. The bonded and the unbonded anchors are shown in Figure 4.

Concrete of compressive strength 30 MPa is intended for the six slab specimens. After the hardening of concrete and reaching compressive strength of average 26.3 MPa after 7 days, the six post-tensioned tendons were stressed: the cubes tested at 7 days of age resulted 23.61, 26.77 and 28.63 MPa.

The jacking force P_j is calculated based on the maximum permissible concrete tensile stresses according to ACI 318-19 [6] provisions which is found to be 459.8 kN. Thus, the prestressing force needed for one tendon is around 154 kN. Tendons prestressing is sequentially performed. The prestressing was done from the “live” end for the six slabs. Table 1 illustrates the elongation measured for the tendons after the application of the hydraulic jack force.

Table 1. The elongation of the tendons after prestressing in mm

Specimen	Tendon no. 1	Tendon no.2	Tendon no.3
UBSR1	33.5	33	34
UBSR2	33	31	32
UBS1	32.5	34	36
UBS2	34	32.5	35
BS1	43	35	36
BS2	34	34	35

From the elongation of each tendon the strain is calculated, followed by the calculation of the stress in each tendon that is converted to a jacking force giving the following results; and the equations used are the following:

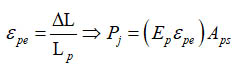
Where, ε_pe is the tendon’s strain, DL is the tendon total shortening, L_p the tendon length, P_j is the jacking force, E is the Young’s modulus of the tendons steel, and A_ps is the tendons cross sectional area. The elongation is obtained from the Table 1, the exact length of the tendon L_p is 4.304 meters and the Young’s modulus of the prestressing tendons E_p is 190,000 MPa. Table 2 illustrates the calculation of the strain in each tendon while Table 3 presents the calculated tendon’s jacking force.

Table 2. Strain calculation in each tendon

Specimen	Strain, tendon 1	Strain, tendon 2	Strain, tendon 3
UBSR1	0.007783	0.007667	0.007899
UBSR2	0.007667	0.007203	0.007345
UBS1	0.007551	0.007899	0.008364
UBS2	0.007899	0.007551	0.008132
BS1	0.007667	0.008132	0.008364
BS2	0.007899	0.007899	0.008132

Table 3. Jacking force calculation in each tendon (KN)

Specimen	Pj  tendon 1	Pj  tendon 2	Pj  tendon 3
UBSR1	145.95	143.77	148.13
UBSR2	143.77	135.08	137.74
UBS1	141.60	148.13	156.85
UBS2	148.12	141.60	152.5
BS1	143.78	152.5	156.85
BS2	148.13	148.13	152.5

2.2. Prestress Losses

The prestressing force losses are calculated according to ACI 318-19 [6] provisions which refers to the Post-Tensioning Institute Manual [3]. The short-term losses are due to elastic shortening, anchorage slippage and friction. While, the long-term losses are due to shrinkage, creep of concrete and relaxation of the tendons. The initial prestressing force (Pi) is thus, the prestressing force after the short-term losses and the effective prestressing force (Pe) is that at the service load stage after all losses. The short-term losses are calculated, starting by the elastic shortening losses, which is given by

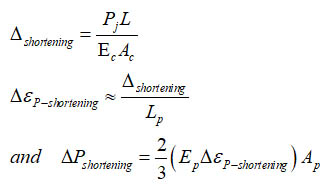
Where, Δ_shortening is the change in length due to the elastic shortening of the concrete slab, L is the slab span, E_c is the modulus of elasticity of the concrete at the initial stage, A_c is the cross sectional area of the slab specimen, P_j is the jacking force, Δε_shortening is the change in the tendon strain due to the elastic shortening, A_p is the cross sectional area of the tendon and ΔP_shortening is the prestressing force loss due to elastic shortening which is multiplied by 2/3 to account for the sequential prestressing. Table 4 illustrates the values of the prestressing losses due to elastic shortening.

Table 4. Values of shortening losses for each specimen

Specimen	Δshortening (mm)	Δεshortening	Δfp-shortening (MPa)	ΔPshortening (kN)
UBSR1	0.57	0.000133	25.2	4.97
UBSR2	0.54	0.000126	23.9	4.73
UBS1	0.58	0.000135	25.7	5.07
UBS2	0.58	0.000134	25.4	5.02
BS1	0.59	0.000137	26.0	5.14
BS2	0.58	0.000136	25.8	5.09

The losses due to anchorage slippage are neglected since after prestressing the six slabs, it was detected that no slippage occurred for any tendon. The last source of the short-term losses is the friction losses, which occurs due to the wobble effect and the curvature effect of the tendons with empirical coefficients for the wobble and the curvature losses defined by the PTI manual [3] as k and μ, respectively. For the unbonded tendons μ and k are considered as 0.07 and 0.001, respectively, while for the bonded tendons they are 0.22 and 0.0075, respectively. The prestressing losses ΔP_friction is calculated at the slab mid-span (x = 2.15 m) by

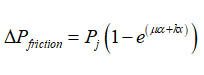
Where α is the angle of tendon curvature in radians. The friction losses due to curvature effect is neglected because the tendon is only inclined by 2^o (the tendon is almost straight). The friction losses are calculated for the six slab and the results are presented in the Table 5.

Table 5. Friction losses values for the six specimens

Specimen	Pj (kN)	Wobble coefficient (k)	ΔPfriction (kN)
UBSR1	437.86	0.003	2.82
UBSR2	416.60	0.003	2.68
UBS1	446.58	0.003	2.87
UBS2	442.23	0.003	2.84
BS1	453.13	0.00246	2.39
BS2	448.76	0.00246	2.37

The short term losses for each slab specimen are added in kilo newton and calculated as percentage from the jacking force and presented in Table 6.

Table 6. Six slab specimen's short term losses values

Specimen	Pj (kN)	ΔPj (kN)	ΔPj/ Pj %	Pi (kN)
UBSR1	437.86	7.79	1.78	430.08
UBSR2	416.60	7.41	1.78	409.19
UBS1	446.58	7.94	1.78	438.64
UBS2	442.23	7.87	1.78	434.37
BS1	453.13	7.54	1.66	445.60
BS2	448.76	7.46	1.66	441.30

2.3. The Transfer Stage

In Table 6, the prestressing force at the transfer stage (considering the short term losses is listed as Pi). Based on this value, the compressive and tensile stresses at outer concrete fibres of the slab mid-span section at the transfer stage is calculated and compared to the limitations defined ACI 318-19 [6] provisions. Based on fʹ^ci = 22 MPa, these limits are -13.2 MPa and 1.17 MPa for the compressive and tensile stress, respectively. The stress at the bottom and top fibres of the mid-section of the slabs are calculated and checked versus the ACI318-19 [6] limits; these are listed in Table 7.

Table 7. Top and bottom stresses for the six slab specimens

Specimen	ftop (MPa)	ACI 318-19 [6] limit (MPa)	fbot (MPa)	ACI 318-19 [6] limit (MPa)
UBSR1	-0.53	1.17	-4.86	-13.20
UBSR2	-0.60		-4.52
UBS1	-0.50		-4.98
UBS2	-0.52		-4.91
BS1	-0.48		-5.09
BS2	-0.50		-5.02

2.4. Instrumentation and Test Set-Up

Strain gauges are used to measure the change in length at different locations on the concrete and the prestressing tendons. Four strain gauges are fixed on each slab. Three strain gauges are fixed on the slab tendons, while one strain gauge is fixed on the concrete top surface of the slab at the mid-span. Two strain gauges are added on two of the three tendons in each slab at mid-span in order to measure the elongation of the tendons from the start of loading till final failure. The third strain gauge is fixed at the dead end of one of the tendons to detect the long-term losses of the prestressed tendons.

The test setup is designed to test the slab in flexure in a four-point loading fashion. Two line loads are applied on the slabs using two HEB 300 beams, which are supported in the transvers direction of the slab. A third HEB 300, 1.60 m long, is supported on the two HEB 300 parallel to the longitudinal direction of the slab (Figure 5). The length of the 1.60 meters HEB 300 is chosen in order to maintain a trapezoidal bending moment matching the tendon’s harped profile. Rubber pads are positioned between the two HEB-300 and the slab specimen. Linear variable differential transducers (LVDTs) are also used to record the deformation of the slab in the mid-span.

3. Results

The six post-tensioned slabs with bonded and unbonded tendons are tested according to the described procedure and setup and some results are obtained. The flexural capacity of the six slabs were calculated theoretically as according to ACI 318-19 design requirements and procedures and compared to the results recorded during the four-point load flexural testing. Firstly, the difference between the theoretical and experimental values was less than 10 percent confirming the accuracy of the planned program and test setup. Secondly, the unbonded post-tensioned slabs with non-prestressing steel reinforcement showed the highest capacity followed by the bonded post-tensioned slabs, while the least capacity was recorded by the unbonded post-tensioned slabs without non-prestressing steel reinforcement. Also, the current adopted equation by the ACI 318-19 for the calculation of the unbonded tendon’s ultimate stress has proven its accuracy still, the limitation of the equation must be checked.

4. Summary

This paper describes an experimental program designed to test post-tensioned slabs with bonded and unbonded tendons. The slabs are tested in flexure to failure in order to compare the stresses in the bonded and the unbonded tendons to each other and the stresses in the tendons to those calculated based on ACI 318-19 [6] for bonded and unbonded tendons.

The aim of this research is to shed light on the validity of the current equation adopted to calculate the stresses in the unbonded tendons at the ultimate limit state. This test has proved its excellent correlation as almost all of the tested slabs have showed a very minor difference between the theoretical and the experimental results. The detailed results of the test and the comparison between the bonded and the unbonded system in addition to the examination of the validity of the ACI 318-19 code equation for calculating the unbonded tendons ultimate stress will be presented elsewhere.

References