International Journal of Civil Infrastructure (IJCI)

ISSN: 2563-8084

1. Introduction

The interaction between surface and deep water bodies, particularly between rivers and their underlying aquifers (the object of this work), is a topic of great interest in hydrogeology due to its importance for the storage and maintenance of underground water resources. Its study not only covers the mechanical problem of the investigation of 2D patterns of water flow, dependent on the contour conditions of hydraulic potential and soil permeability, but also extends to the temperature patterns determined by the coupling between water flow and heat transport imposed by temperature conditions at the surface and at the bottom of the domain.

Numerous works, most of them dedicated to in situ studies (Duque et al. [1]), have been published in the last decades. There are no analytical solutions other than for 1D cases of constant vertical flow (1D) and harmonic surface temperature conditions (Bredehoeft & Papadopulos [2] and Taniguchi [3]). The study of vertical temperature profiles has recently been used in the form of an inverse problem to determine recharge-discharge rates that are difficult and expensive to obtain by other means (Duque et al. [4]).

In consolidated soils, to a greater or lesser degree, the hydraulic permeability anisotropy can become important, with values of the ‘horizontal/vertical permeability’ ratio greater than 10 (Childs et al. [5] and Chapuis and Gill [6]). As a consequence, the velocity field (decoupled from the thermal problem) and the temperature field (coupled to the previous one) are strongly dependent on this quotient.

In the present work, a symmetric, 2D scenario composed of a river and its underlying aquifer with a thickness less than half the horizontal extension is investigated by means of numerical simulations using the network simulation method (Horno [7] and García-Ros et al. [8]) and the free software Ngspice ([9]).

The boundary conditions of constant piezometry of the river, large permeability at the bottom of the aquifer, and free condition at the right edge produce 2D flow patterns in which the development region of the linear (mean temperature) profile can be clearly distinguished. The extension of this region, clearly influenced by anisotropy in permeability, spreads as the ratio ‘horizontal/vertical’ permeability increases and can reach the right boundary deleting the formation of eddies.

In addition, the combination of the heat transported by dragging and the harmonic variation of the temperature imposed on the up and down surfaces produces the generation of thermal waves or eddies that moves along the domain towards the outlet direction. According to the magnitude of the flow field, which in turn is strongly dependent on the ‘horizontal/vertical’ permeability ratio, the region more influenced by the river temperature extends (as velocity increases) towards the outlet up to reach all the domain. The mean temperature-depth profiles are very changeable and difficult to characterize.

2. Physical, Mathematical and Network Models

The physical scheme of the problem (symmetric) is depicted in Figure 1. Temperature and flow boundary conditions are shown in this figure. A river with constant hydraulic (height) head discharges on the sub-soil aquifer whose bottom and vertical right boundary are permeable (outflow water) while the left boundary is impermeable (no flow). Vertical and horizontal components of the velocity are very different from one point to another depending on the anisotropy in the hydraulic conductivity.

A seasonal (annual) harmonic temperature is imposed at the upper region (soil surface) while the temperature of the river-water is constant. Vertical left boundary is adiabatic to reflect the symmetry of the scenario, the bottom maintains a constant value temperature and finally, the right vertical boundary is free to flow (heat is dragged by the water according to its temperature at the boundary).

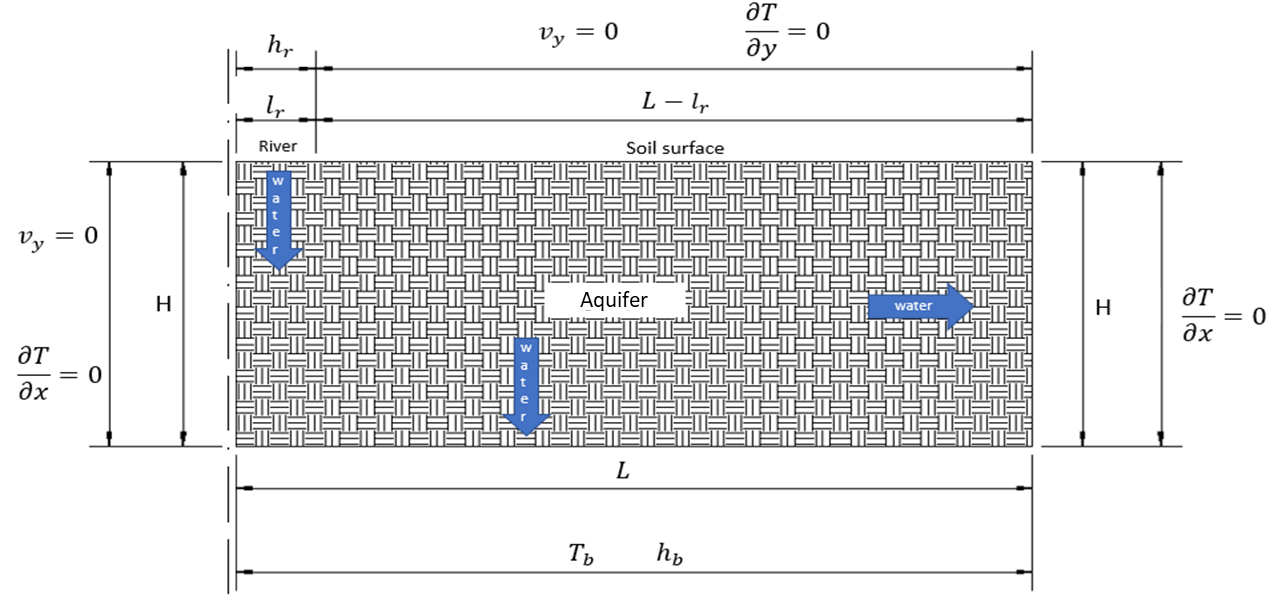
As for the mathematical model, rectangular coordinates with the origin at the upper-left corner of the aquifer are chosen (see Figure 1). The list of equations is as follows

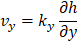
Eq. 1, Darcy constitutive law, is decoupled from the heat transfer. In this equation, k_x and k_y (m/s) are the horizontal and vertical hydraulic conductivities respectively, while h (J/N) represents the piezometric head.

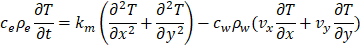
Eq. 2, is the balance of the different heat flows (convection, conduction and storage) that locally counteract one another (heat conservation flow). Fourier law is used for the conduction flow. The term c_eρ_e (calg⁻¹°C⁻¹) is the specific heat of the water-soil matrix, k_m(cals^-1m^-1°C^-1) is the thermal conductivity of the water-soil matrix, c_wρ_w (calg⁻¹°C⁻¹) is the specific heat of water, v_x and v_y are the horizontal and vertical components of the water velocity, and T (°C)  and t (s) the temperature and time variables.

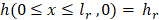
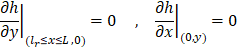
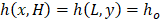
As regards the flow boundary conditions, Eq. 3a is a Dirichlet condition for the head variable along the river. In this equation, l_r (m) is the width of the river and h_r (J/N) its piezometric head. Eq. 3b is the no-flow condition at the ground surface and at the symmetric vertical wall, and Eq. 3c is again a first class condition that emulates the constant head h_o (J/N) at the outflow regions (bottom and right limits) of the aquifer. Temperature boundary conditions are described in Eqs. 4a, 4b and 4c.

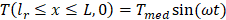
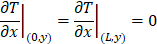
A first class condition is imposed at the river-water, Eq. 4a, where T_r (°C) is the constant river temperature and at the ground surface. In Eq. 4b, surface soil temperature is dependent according to annual harmonic variation. A pure sinusoidal dependence has been chosen for simplifying. T_med (°C) is the average soil surface temperature while ω (rad/s) is calculated as 2π/τ, with τ the period of the oscillation. Homogeneous second class or Neumann condition is imposed at the symmetric (adiabatic) line (no heat flow), Eq. 4c, while the right vertical boundary is assumed free, which means that flow dragged the heat according to the local temperature at the boundary. Temperature at the bottom (Eq. 4d) T_o is constant (°C).

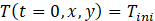
Finally, Eq. (5) represent the initial temperature, T_ini (°C).

This scenario has been adopted as typical without prejudice to the fact that real scenarios may be slightly or substantially different. Thus, it is common to find aquifers with an impermeable bottom and shallow aquifers, for which the boundary conditions are different. The initial temperature does not affect the final solution of the thermal field (steady state). The problem described by the mathematical model represents a unique case in which the most important deviations of the temperature field occur in a region of the aquifer close to the river bank. Beyond this region, whose extension would be interesting to determine, there are vertical temperature profiles where the recharge effect is not appreciated. These profiles represent the maximum or minimum value of the temperature that is reached at each point. From the mathematical point of view, the application of any other boundary condition does not present special difficulties from the point of view of numerical calculation.

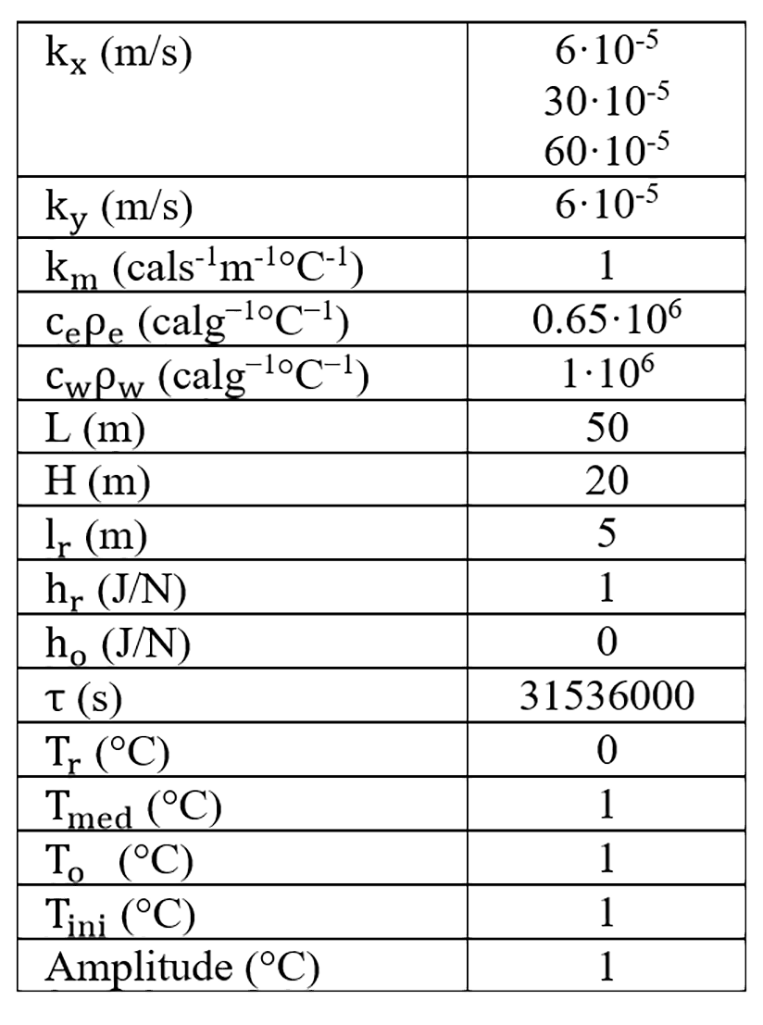
The problem parameter values are listed in Table 1. Anisotropy in the hydraulic permeability is imposed by increasing its horizontal value 5 and 10 times in relation with the vertical value which retains a same value.

The design of the numerical model follows the rules of the network simulation method, a tool largely employed in the literature to solve many types of coupled, non-lineal similar or even more difficult scenarios (such as Bénard, Yusa and many others) that the one here studied. Really, the numerical model is a simple modification of the software ‘Fahet’ (Alhama et al. [10]), developed by the research group of the UPCT and applied for the solution of some benchmark problems (Alhama et al. [11]).

As we consider the network model as an auxiliary tool, we refer to the cited references to deepen in its design. A mesh grid of 100 X 20 cells has been used. The time step varies according to the smoothness of the solution and its values are ruled by the software according to the tolerance chosen by the user. Other parameters of the simulation are pointed out later.

Table 1. Parameter values of the problem

3. Numerical Solution

3. 1. Patterns of equipotential and flow lines

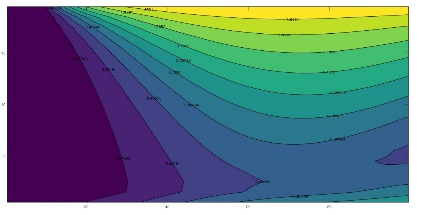
Preserving the geometric scale of the domain, Figures 2 and 3 show the patterns of iso-potentials and streamfunction, respectively.

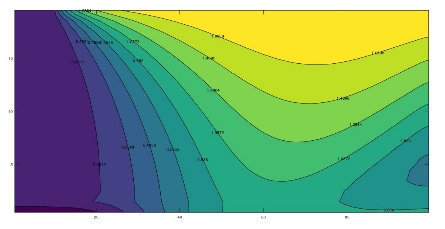
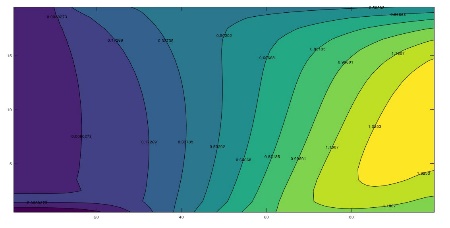
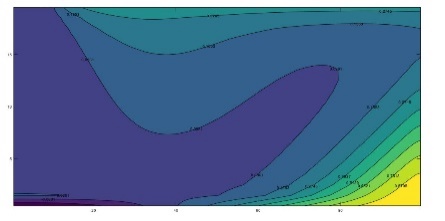
For the isotropic case (Figures 2a and 3a), it can be seen that, as expected, most of the flow is directed towards the bottom of the aquifer and in the area under the river. In fact, 90% of the total flow from the river is located in the region 0 <x <l_carac However, it is important to note that neither the vertical nor the horizontal velocity of the fluid (which are relatively similar) in the left central region of the aquifer can be neglected, these give rise to strong couplings between the water and heat flows in this region. Beyond, to the right of the aquifer, the same phenomenon occurs, although with already negligible velocities, which induces standard vertical profiles practically independent of flow. On the other hand, it is noted that the discharge velocity at the bottom of the river changes with position, which confirms as the most suitable choice of the boundary condition that of constant hydraulic potential instead of that of constant velocity.

The effect of anisotropy on permeability can be seen in Figures 2b and 3b (for K_x = 5k_y) and 2c and 3c (for k_x = 10k_y). As expected, the equipotential lines expand as the permeability ratio increases, although the line with the lowest potential remains within the domain due to the null potential condition at the right edge. The flow lines are more illustrative since they show that much of the water flow exits the right edge of the domain for increasing horizontal permeabilities. In fact, for k_x = 10k_y, more water comes out of the right border of the domain than at the bottom. The vertical and horizontal components of velocity can be seen through the slope of these lines

(a) k_x = k_y

(b) k_x = 5k_y

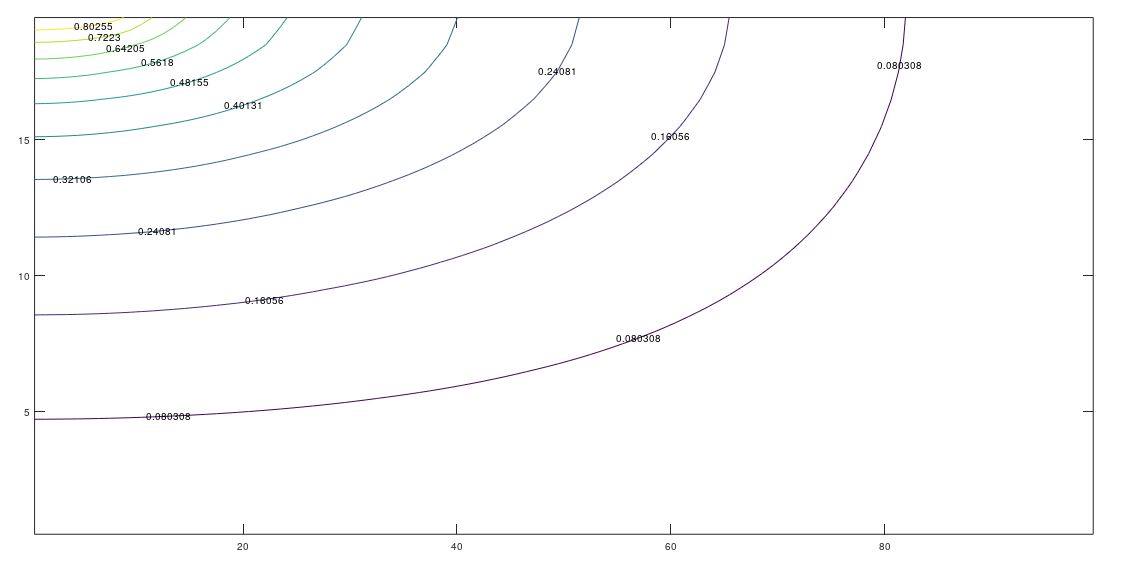
(c) k_x = 10k_y

(a) k_x = k_y

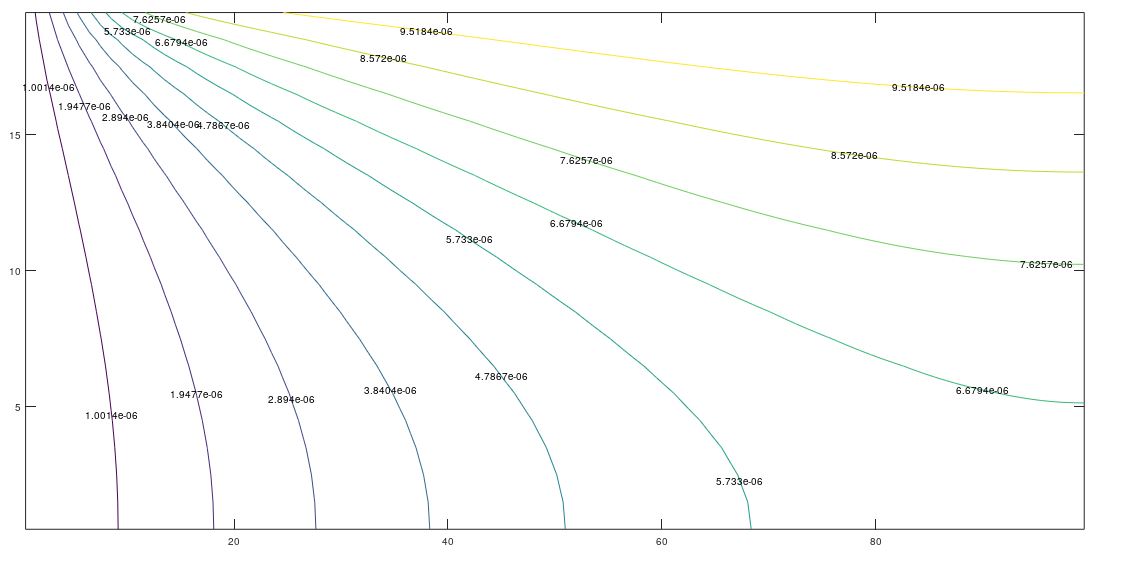
(b) k_x = 5k_y

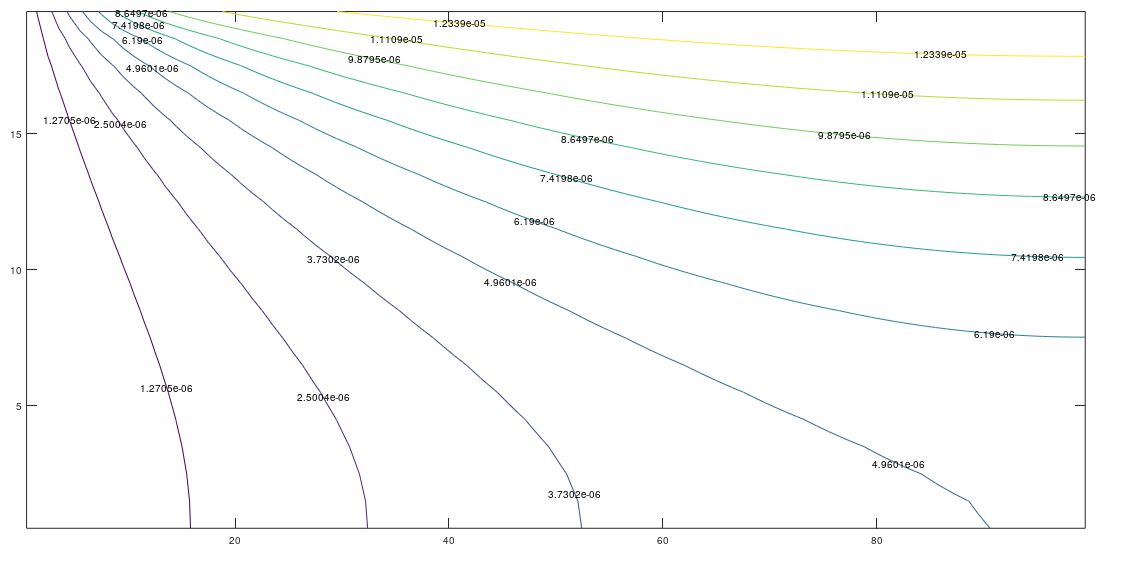
(c) k_x = 10k_y

From a negligible horizontal velocity almost throughout the domain for the case k_x = k_y, it passes to the emergence of wide regions where the horizontal velocity is appreciable for substantially higher horizontal conductivities. However, a central domain seems to be maintained in which horizontal and vertical velocities are comparable.

It can be affirmed that, in domains that are horizontally extensive enough, the isotropic case gives rise to a well-defined extension region in which the thermal profiles (of average temperature) will develop until a linear profile is reached. Beyond this region, velocities can be considered negligible and such thermal profiles invariant and linear.

The anisotropic case extends this characteristic length and can reach the right vertical border, which eliminates the linear thermal profile region for the mean temperature.

3.2 Patterns of isotemperature-time

To illustrate the complex variation of the time-temperature patterns in which the harmonic displacement of the heat islands or eddies is represented, Figure 4 shows these patterns for eight different times within the same annual period, once the initial transient has been overcome. In all cases these figure shows the emergence, development and fading of the islands of hot and cold temperatures which displace throughout the domain. For k_x = k_y (Figure 4), there is negligible horizontal water flow and the islands move vertically towards the surface and bottom of the aquifer while for k_x >> k_y, the appreciable horizontal flow force the islands to move also towards the right boundary (Figures 5 and 6).

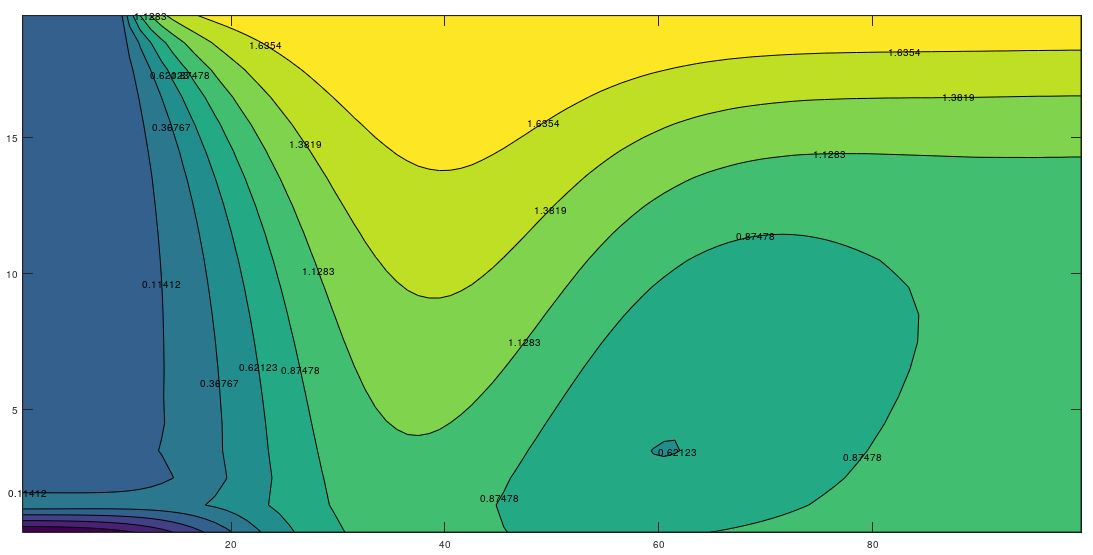
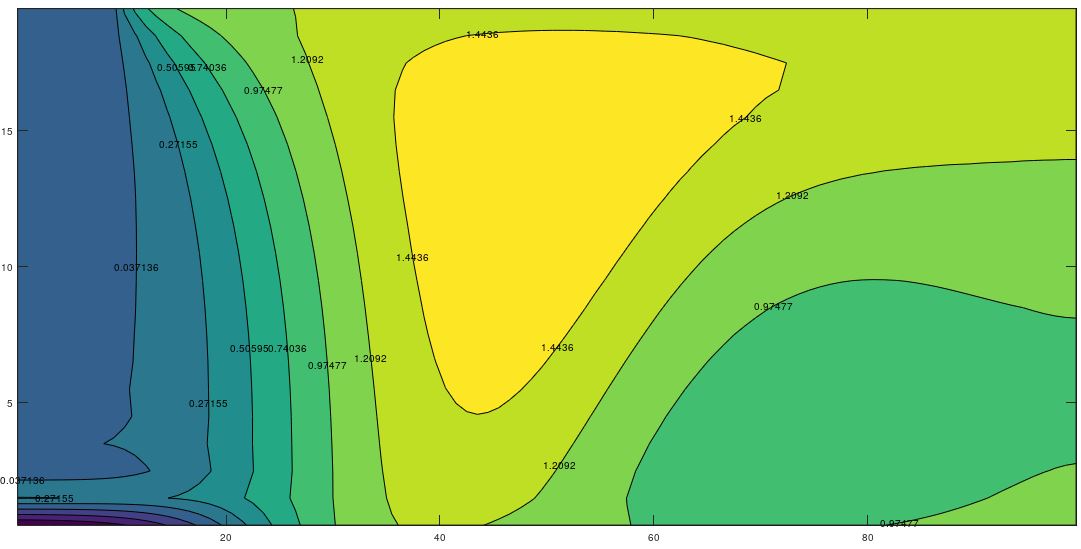
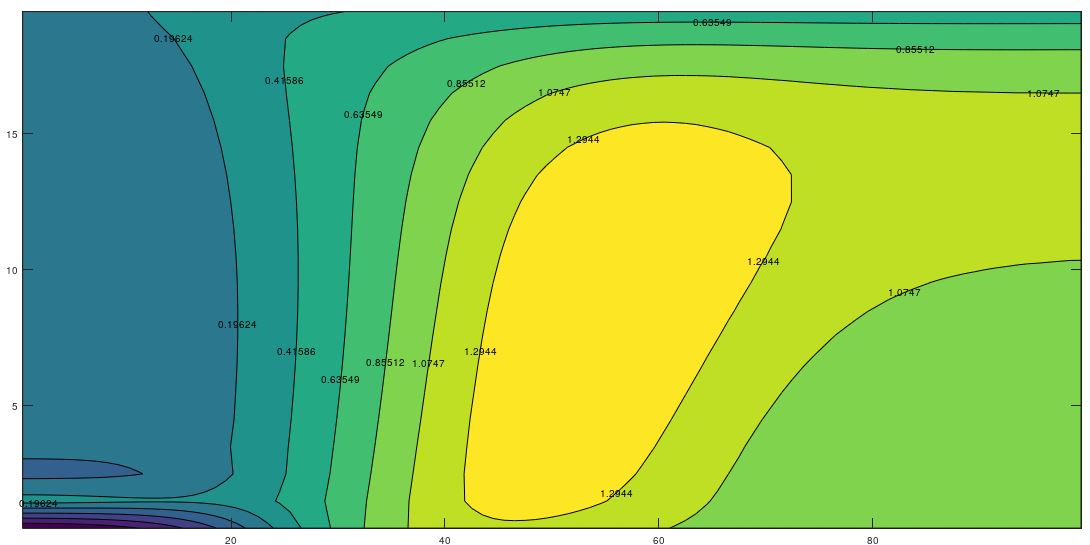
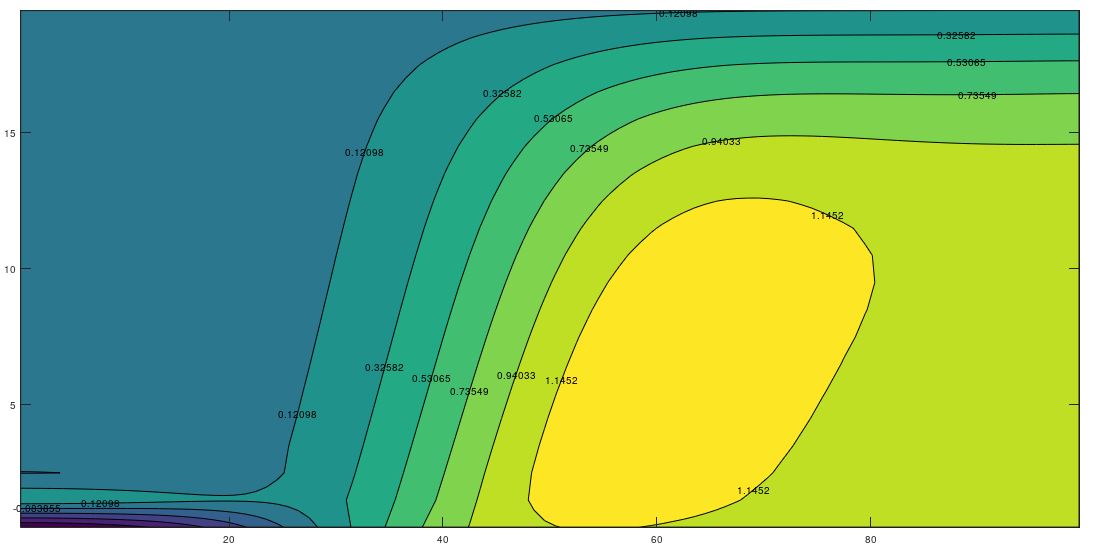
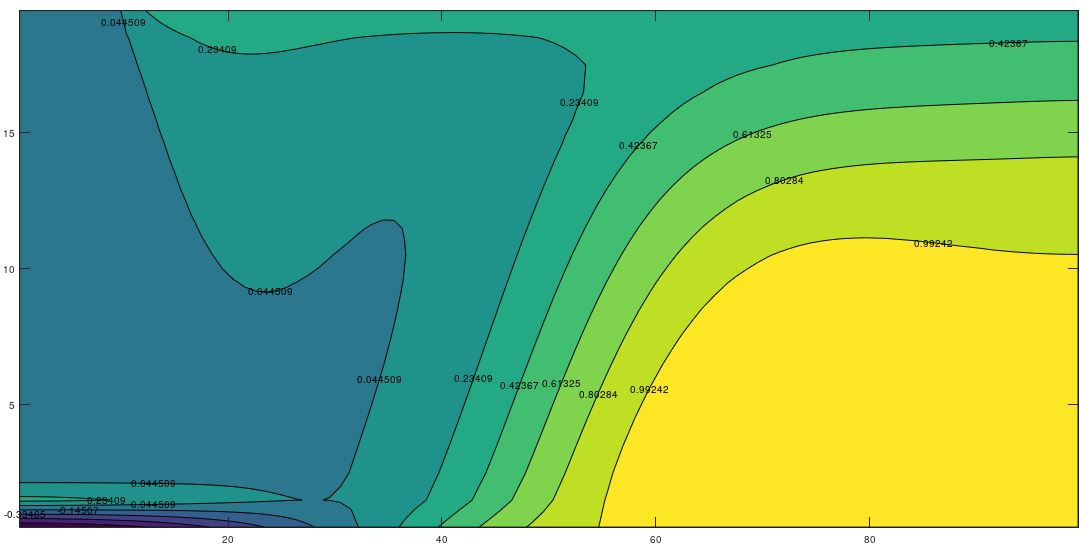
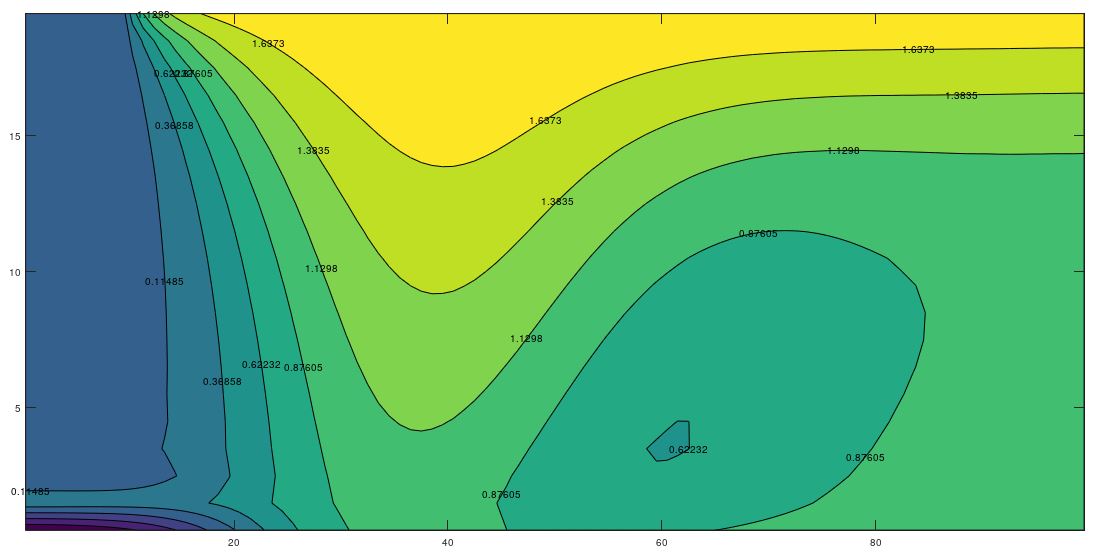
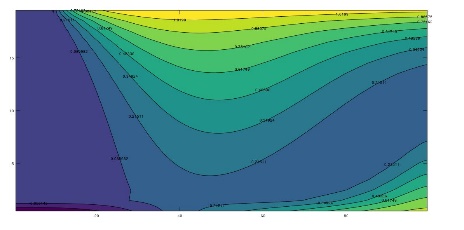
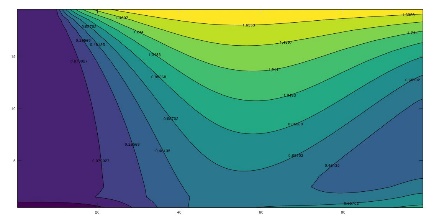
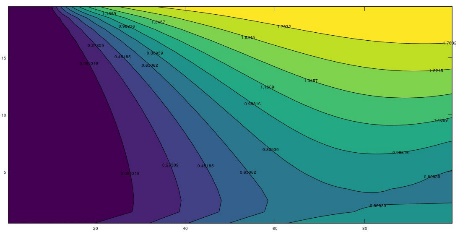
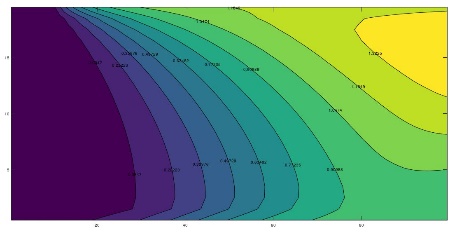
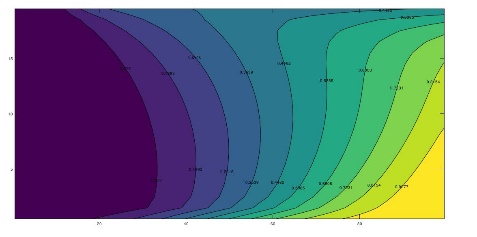
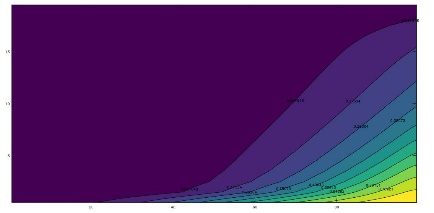
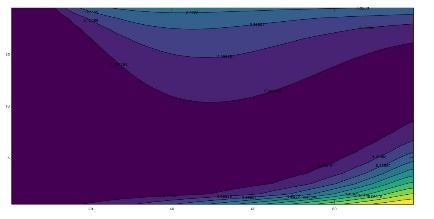
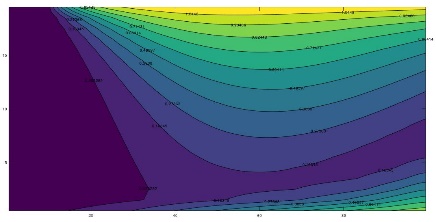
3.3 Temperature Profiles

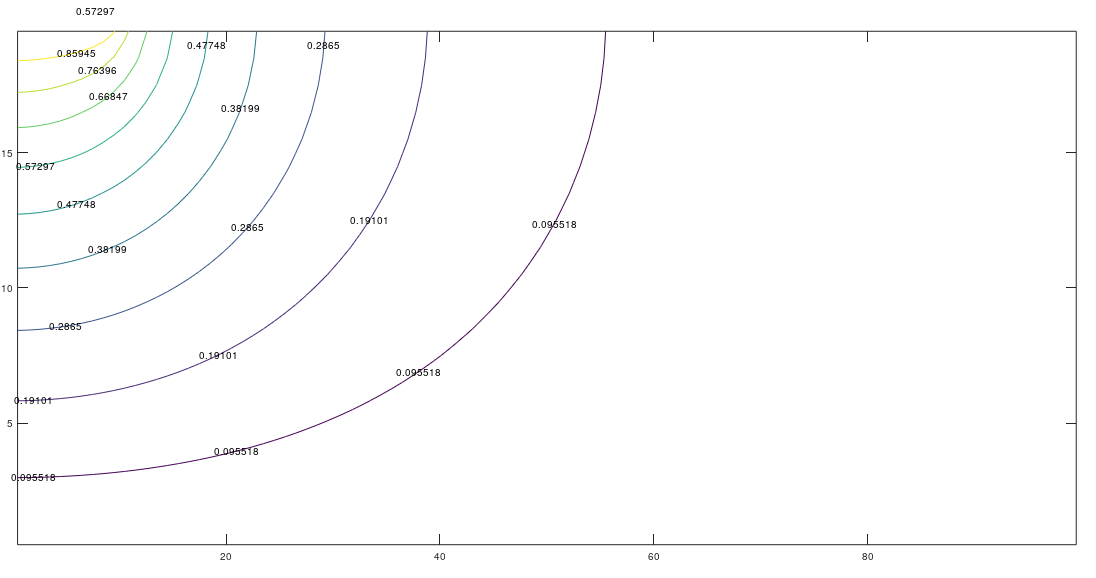
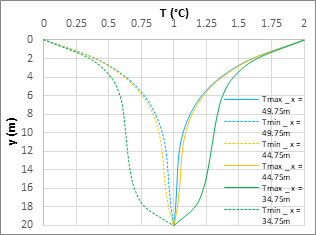
Figures 7 represents the maximum and minimum values of the temperature along different vertical columns within the aquifer. Three locations, all far from the river have been chosen. In the case of k_x = k_y, Figure 7a, the profiles are nearly symmetric, and the small difference between the location x = 44.75 m and x = 49.75 m is justified in that these locations are beyond the characteristic region in which the profiles develop.

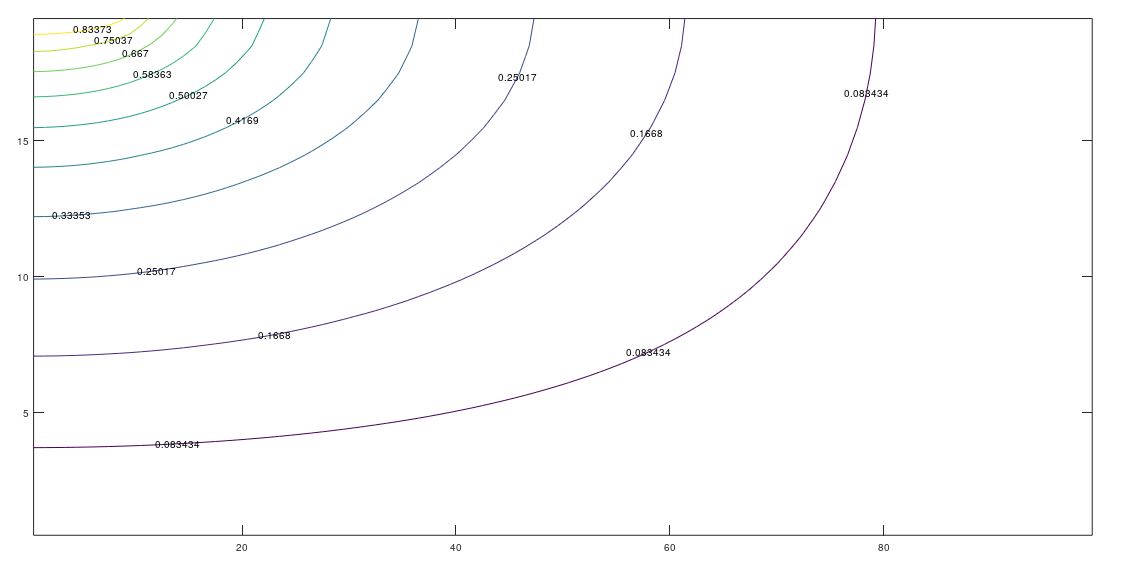
For k_x = 5k_y (Figure 7b) the profiles have lost their symmetry because they are within the region of their development. The same occurs for k_x = 10k_y. The temperature T_min is close to that of the river, an effect more accused for k_x = 10k_y, Figure 7c. As regards T_max, the profile is more difficult to explain because the locations x= 34,75 m and 44,75 m fall within the profile development region where the coupling is strong.

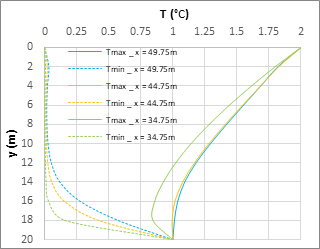
These explanations are coherent with the profiles of mean temperature, Figure 8. For k_x = k_y, the profile is quite lineal just at the boundary and curves smoothly below such locations. The same occurs for k_x = 5k_y and k_x = 10k_y, but with profiles that are clearly curved. Due to the temperature boundary condition at z=H, the mean temperature converges in all cases to the bottom temperature forcing the profile to be bent near the bottom. Really, boundary equation (4d) can be considered as an idealized condition since it would be applied below the aquifer bottom in most cases.

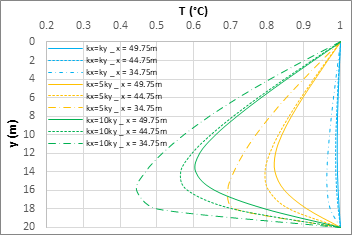
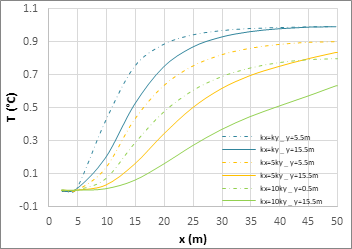
Finally, Figure 9 shows the horizontal temperature profiles in two typical positions, y = 5.5 m (dashed line) and y = 15.5 m (continuous line). Again, this region shows the existence of a horizontal developing region, small than the length of the domain for k_x = k_y (where the temperature tends to its mean value whatever be the depth coordinate) and larger for k_x > 5k_y or 10k_y, (where the mean temperatures tend to a different value according the depth because the developing region is larger than the length of the domain).

(a) k_x = k_y

(b) k_x = 5k_y

(c) k_x = 10k_y

4. Final Comments and Conclusions

The interaction between rivers and underlying aquifers in order to determine the recharge-discharge between them, knowing the piezometric conditions of the contour, to determine the velocity field is already a complex problem that requires numerical solutions.

Flow patterns are basically determined by the permeable or non-permeable nature of the aquifer bottom and the anisotropy in hydraulic permeability that can be pronounced in consolidated soils. The flow field is coupled to the heat transport problem, resulting in temperature patterns that can still be higher under the condition of harmonic temperature on the ground surface.

For cases of aquifers that are more or less extensive horizontally and with permeable bottom, the numerical simulations carried out show the emergence of a horizontal extension or characteristic length in which a linear profile of average temperatures that prevails beyond this length progressively develops. The increasing anisotropy of the soil, defined by the 'horizontal / vertical permeability' ratio, which can reach values of several tens, increases the size of this region of development of the linear profile and gives rise to more or less regular profiles of mean temperature dependent on the anisotropy within this region.

However, the maximum and minimum temperature profiles, of more complex interpretation, apparently lack regularity thanks to the strong coupling between flow and heat transport. These profiles curve and converge to the idealized boundary condition imposed by the temperature at the bottom. Thus, the T_med profiles are the only ones capable of being used in the inverse problem of the determination of velocities and flows from the experimental knowledge of the profiles

The strong coupling of flow and heat transport, on the other hand, translates into the emergence of heat islands or eddies that evolve from the central region of the aquifer towards the horizontal boundaries and flow outflow due to diffusive and drag effects. Finally, the horizontal temperature profile highlights the existence of a profile development length that, eventually, can go beyond the right border for large anisotropies.

5. Acknowledgements

We would like to thank “Fundación Séneca” for the scholarship awarded to José Antonio Jiménez Valera, which will allow us to continue this investigation. “21271/FPI/19. Fundación Séneca. Región de Murcia (Spain)”

References