1. Introduction

Distinguishing soils and characterizing them is one of the first steps in geotechnical design. In large projects, the number of field investigation can easily reach hundreds and how one organizes and extract information from these data can be the key for success. Statistical analysis can be implemented to help dealing with a large dataset. One of the goals of this work is to identify two kinds of soils of same origin and thus very similar: saprolitic soil of dolomitic phyllite and residual soil of dolomitic phyllite.

Cluster analysis [1] is a widely used method to categorize data based on its properties. In the field of geotechnical engineering, it is commonly used with Cone Penetration Test (CPT) data for various purposes. For instance, in [2], a review of soil classification based on CPT data is presented, along with a novel methodology that employs the kernel k-means algorithm and artificial neural networks for soil classification. In [3], a cluster analysis technique is utilized to group CPT data based on normalized cone resistance, friction ratio, and soil behaviour index, which led to layer grouping used later to determine soil rigidity model. Additionally, cluster analysis has been used to improve total weight prediction [4], classify different types of phosphogypsum in a stack where the Soil Behaviour Type system (SBT_n) was not effective [5], and group soil layers, delineate lenses and outliers within a sub-layer [6]. Despite the objective of grouping, each of the cited examples employs a specific mathematical approach, such as K-means, Gaussian Mixture Model (GMM), or Fuzzy C-means. In the present study, the K-means method is utilized to identify two soft soils.

2. Site and Data Description

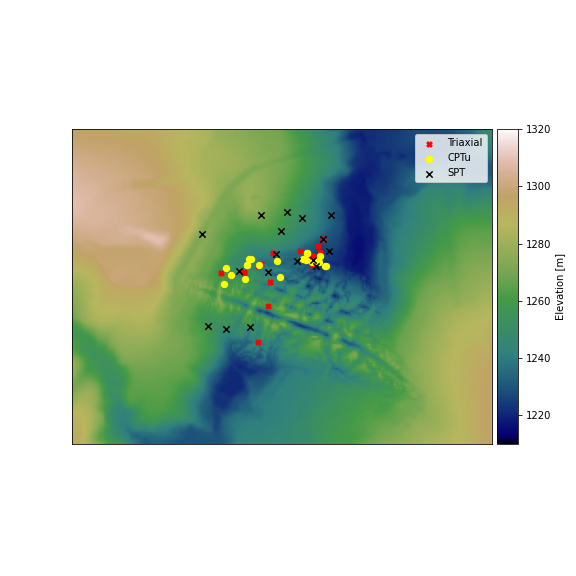
This case of study refers to materials existent on the offset of a tailings dam located on the Quadrilátero Ferrífero, an iron ore rich area located in the state of Minas Gerais, southwest of Brazil. To successfully move into the second phase of construction, it's crucial to identify and characterize the soft materials present at the foundation of the tailings dam. These materials were identified on the downstream rise of the structure on the left abutment, making it necessary to thoroughly understand their properties before proceeding. By doing so, the construction team can ensure that the project is built on a stable foundation, minimizing the risk of future issues. Although there are hundreds of surveys, the present study focuses on the data localized in the interest area. The available data in this area is presented in Figure 1, where the red squares represent laboratory samples (triaxial tests and characterization tests – Atterberg limits and granulometric distribution), the yellow circles represent cone penetration tests with measurement of pore pressure, and the black cross represents standard penetration tests.

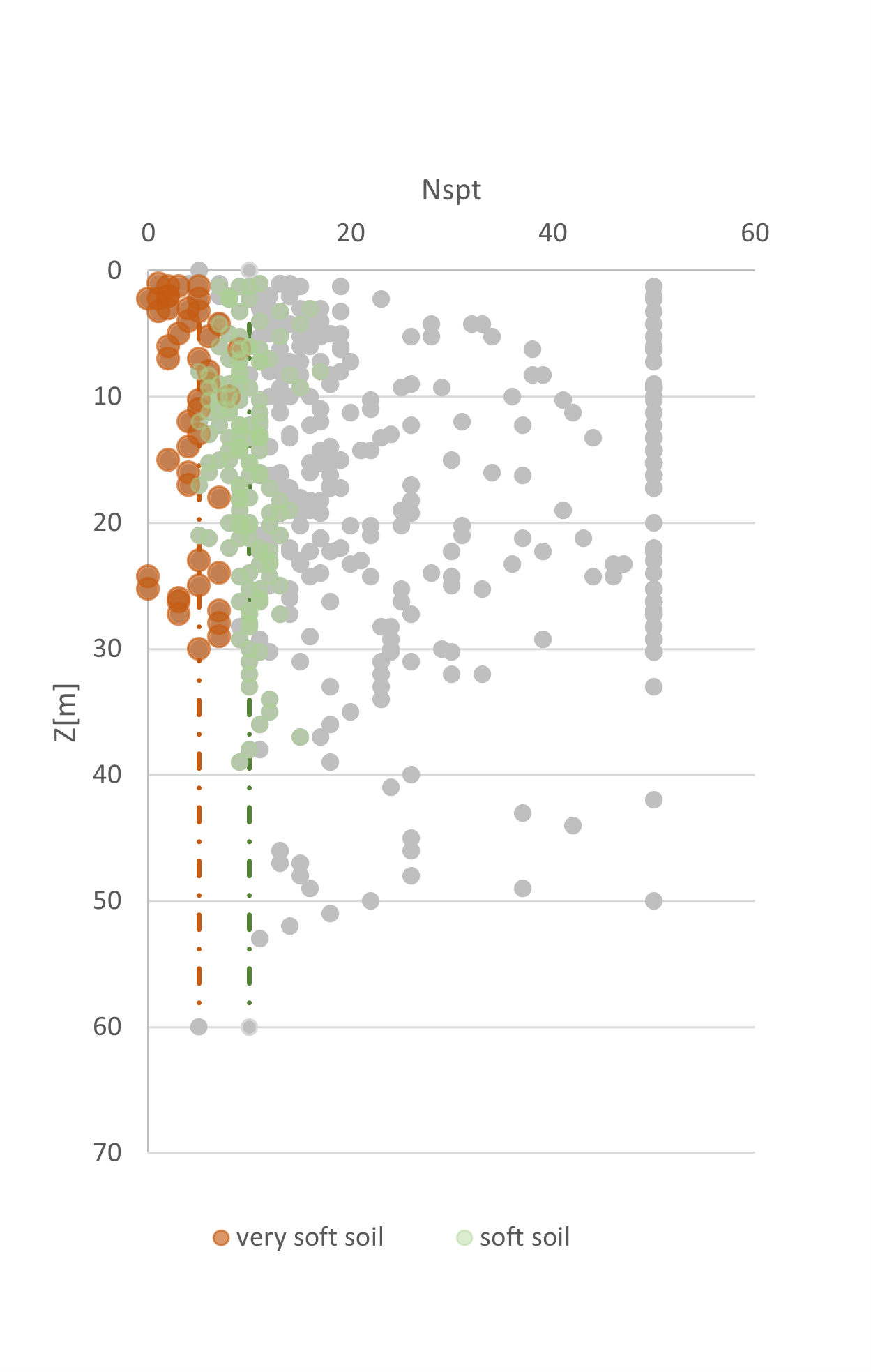
Some of the standard penetration tests (SPT) have reached NSPT blow as low as its own weight, revealing a very soft soil that could not be limited to a specific layer, as shown in Figure 2, where the number of blows (N_spt) are plotted against the depth. The goal of this work is to identify these soils in CPT results and to understand its spatial distribution.

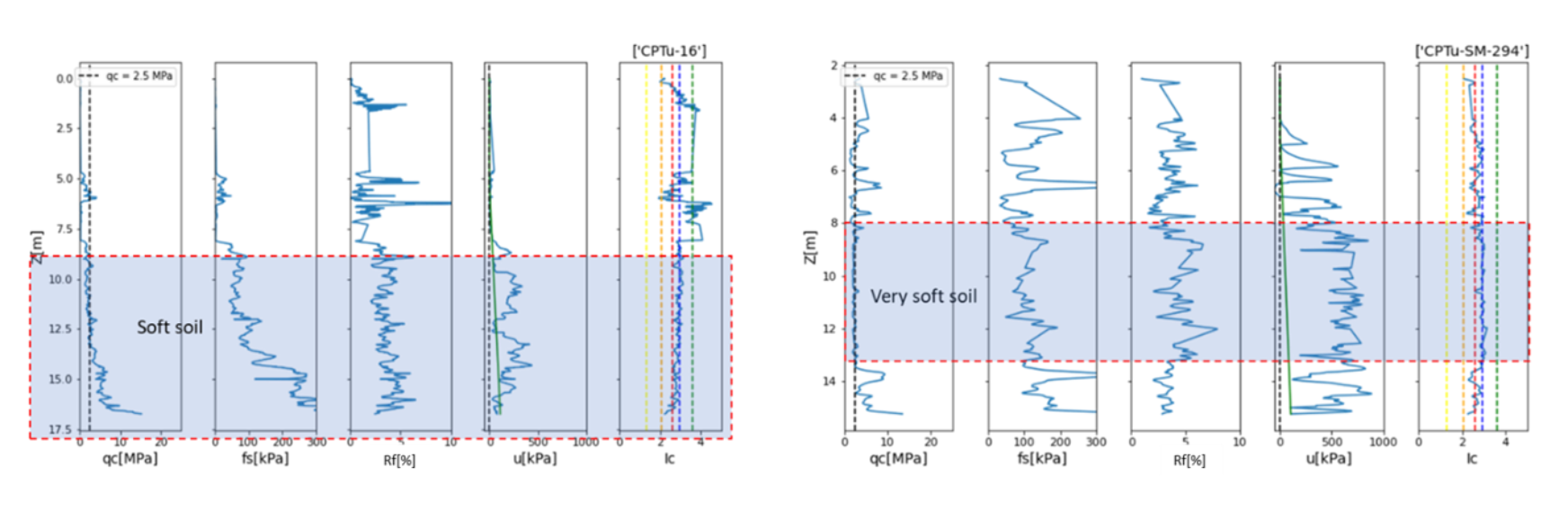
To deal with the large amount of data, all information was treated with an opensource programming language, allowing the standardization and fast treatment of all data. The CPT data were analyzed following the approach in [7]. Figure 3 shows an example of the CPT data with identification of the investigated soils, using SPT investigations existent on the area to confirm the layer zone. For some CPT, the water level was not clear, and a sensitive analysis of the influence of a wrong estimation of the water level in the apparent overconsolidation ratio (OCR) was performed. OCR was defined as:

(1)

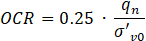
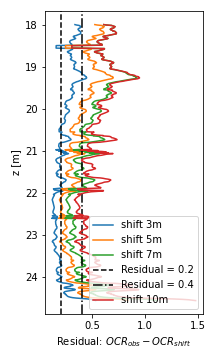
It was possible to see that a wrong estimation of the water level within 3m would impact in a difference in the OCR value about 0.2 to 0.4, as shown in Figure 4. This figure shows the comparison of residuals for different values of the water table. The residual is determined by the difference between the value of the OCR parameter calculated through CPT correlations that consider the water table level provided by the CPT dissipation test (or its indication in the nearest drilling report) and the OCR value obtained when an increase (shift – always deeper) is made in the value of the water table, of 3m, 5m, 7m or 10m.

3. K-Means Method

In this study, the K-means method was applied to group laboratory samples and later, to group CPT data. The K-means algorithm [1],[8],[9] clusters the n data points into K disjoint clusters C, defined as input from the user. The grouping is performed by minimizing the distance from the sample point, x_i to the group centre (mean of the samples, μ_j), known as the inertia or within-cluster sum-of-squares criterion.

(2)

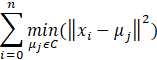
4. Results

4. 1. Laboratory Data

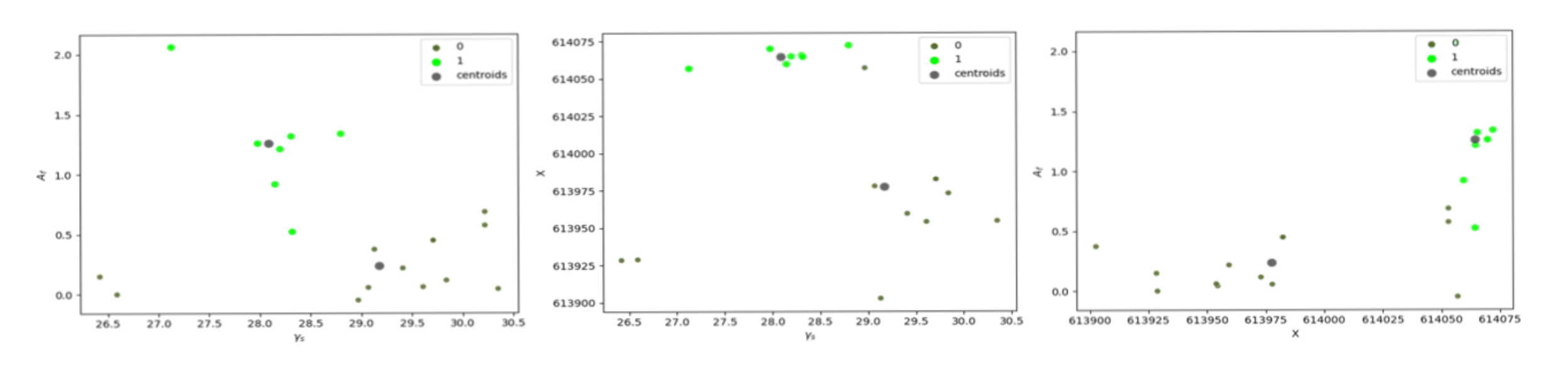
Atterberg limits, granulometric distribution, specific weight of particles and undrained triaxial tests were analyzed to distinguish the two materials and to find any parameter that could be chosen as a flag for each material. The selection of the parameters used to perform the cluster analyses was based on the Principal Feature Analysis (PFA) [10] that selects a subset of the original features that contains most of the essential information. Several combinations of features were tested, and the select features were the pore pressure Skempton parameter at failure A_f, the specific weight of solid particles γ_s, and a spatial variable, the X coordinate of the location where the sample was collected. The number of clusters was set to two, since the goal was to separate the sample within the two soft soils. Figure 5 presents the scatter plot for all features in the three planes where the points are colored by the result from the cluster analysis. Cluster 1 (light green) represent a material with lower specific weight of solid particles and higher pore pressure A Skempton parameter at the failure.

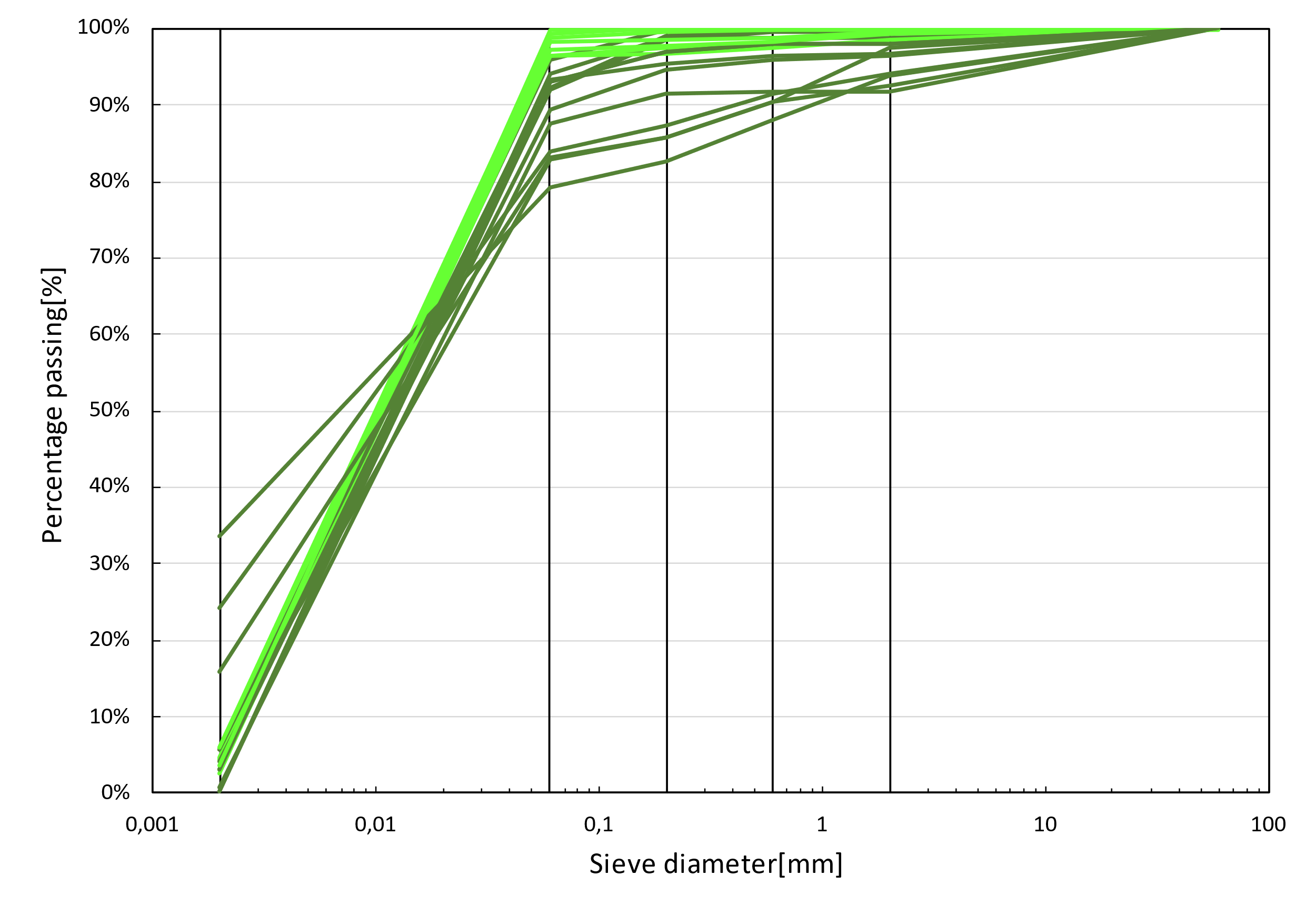
From the granulometric curve in Figure 6 and the ternary diagram in Figure 7 b) it is possible to see that this material is mainly silty. The Casagrande plasticity chart presented in Figure 7 a) offer little assistance in distinguish these materials, since they are quite mixed in this chart, the non-plastic materials are mapped as Ip=LL=0 (points at origin of the graph).

The data from triaxial undrained tests were treated according [11], where the stress paths are presented in the axis:

(3)

(4)

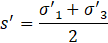
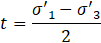
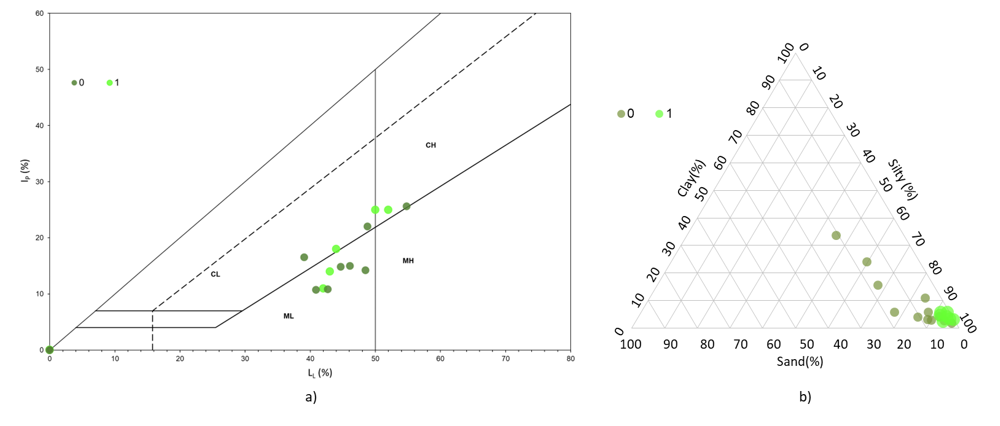
With σ’₁ and σ’₃ being the major and minor principal effective stresses. The pore pressure A Skempton parameter is defined as:

(5)

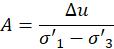
In Figure 8 a), the stress paths are plotted for all samples and in Figure 8 b) the pore pressure A Skempton parameter is displayed as a function of t. In both figures the samples are colored according to the group resulting from the cluster analysis. One can see that the cluster 1 shows a contractile soil with higher pore pressure A Skempton parameter, while cluster 0 shows the opposite.

4. 2. CPT Data

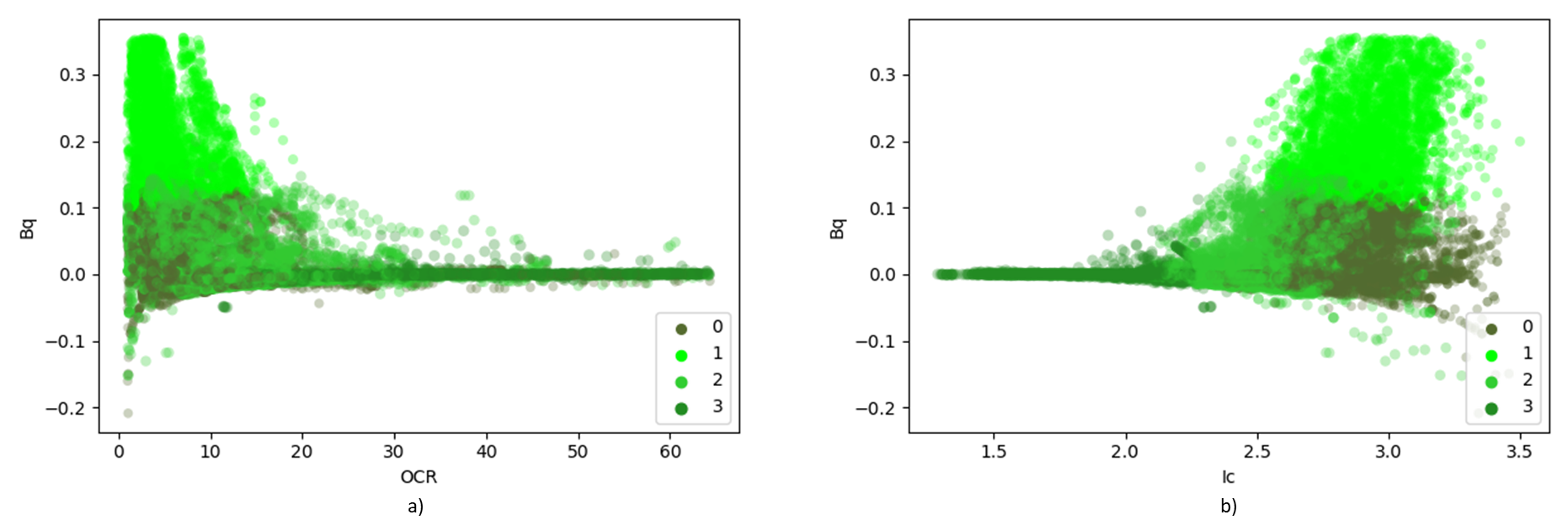
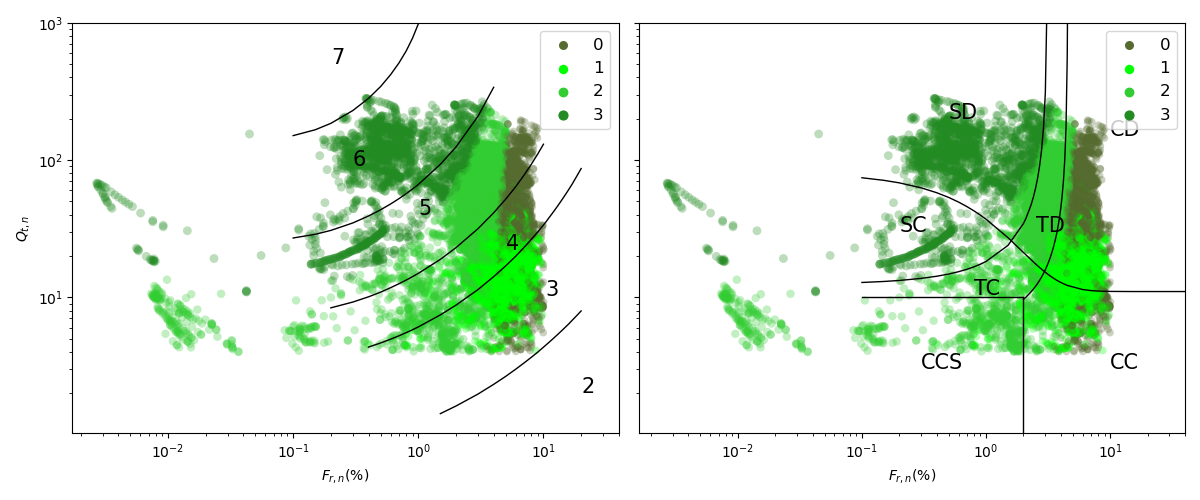
The CPT data shown in Figure 1 was treated following [7] and a cluster analysis analog to the one used on the laboratory tests data was also applied to the CPT data. The goal of this section was to find the soft and very soft soil identified on SPT and triaxial samples in the CPT data. Three tests were performed with the same variables as features: pore pressure ratio Bq; soil behavior index Ic; and friction ratio Fr. The difference in the tests was the number of clusters to form, and since it was not possible to know in advance the exact number of soils presented in the CPTs (which included soils other than the 2 of interest), simulations were conducted varying from 3 to 5 clusters (groups of soils). All tests created a group for soil with low tip resistance (q_c ≤ 5Mpa), low OCR, and high pore pressure ratio.  Figure 9 shows the result for the test with 4 clusters, in terms of a) cone resistance, q_c, b) friction ratio, F_r , c) pore pressure ratio, B_q,  d) soil behavior type index, I_c, e) apparent overconsolidation ratio, OCR, and f) the 3D distributions of the clusters. The group mentioned above is identified as cluster 1 (light green). Cluster 1 could be the very soft soil identified in the laboratory samples (cluster 1 in Figure 8). The only issue in this classification would be the I_c parameter, that is in the range of 2.8-3.5, suggesting a material with silty clay to clay behaviour, while the granulometric distribution of the soil of interest shows up to 95% of silt. Is important remember, though, that the I_c is a behaviour type index, and regardless the soil being almost integrally silty, due to some structure or even the presence of a relatively small percentage of clay it could easily present a response to the probe penetration like a clay or silty clay. This group could not be assigned as the soft soil (cluster 0 in Figure 8) due to the elevated pore pressure generated during to the penetration of the probe, since the laboratory tests showed lower pore pressure A Skempton parameter at failure. In addition, when comparing adjacent SPT and CPT, it is possible to understand that the major difference between the soft and very soft horizons is indeed the pore pressure, as shown in Figure 3, where for the very soft soil the excess pore pressure is higher than 500 kPa. Figure 10 illustrates the relationship between the pore-pressure ratio B_q, and the OCR and I_c parameters. As shown in the figure, cluster 1 exhibits a non-linear trend on these plots, tending towards zero asymptotically as the OCR and I_c values increase. This observation suggests that as the OCR and I_c values increase, the effect of pore-pressure ratio B_q on the material decreases, indicating a lower susceptibility to liquefaction.  The data was plotted on the normalized CPT Soil Behaviour Type chart [7], as shown in Figure 11. The plot reveals that cluster 1 is distributed across the transition zone and clay-like materials, with some points positioned in the zone of sensitive clays. This observation suggests that the material's behaviour could vary, indicating the need for further investigation to determine its properties accurately.

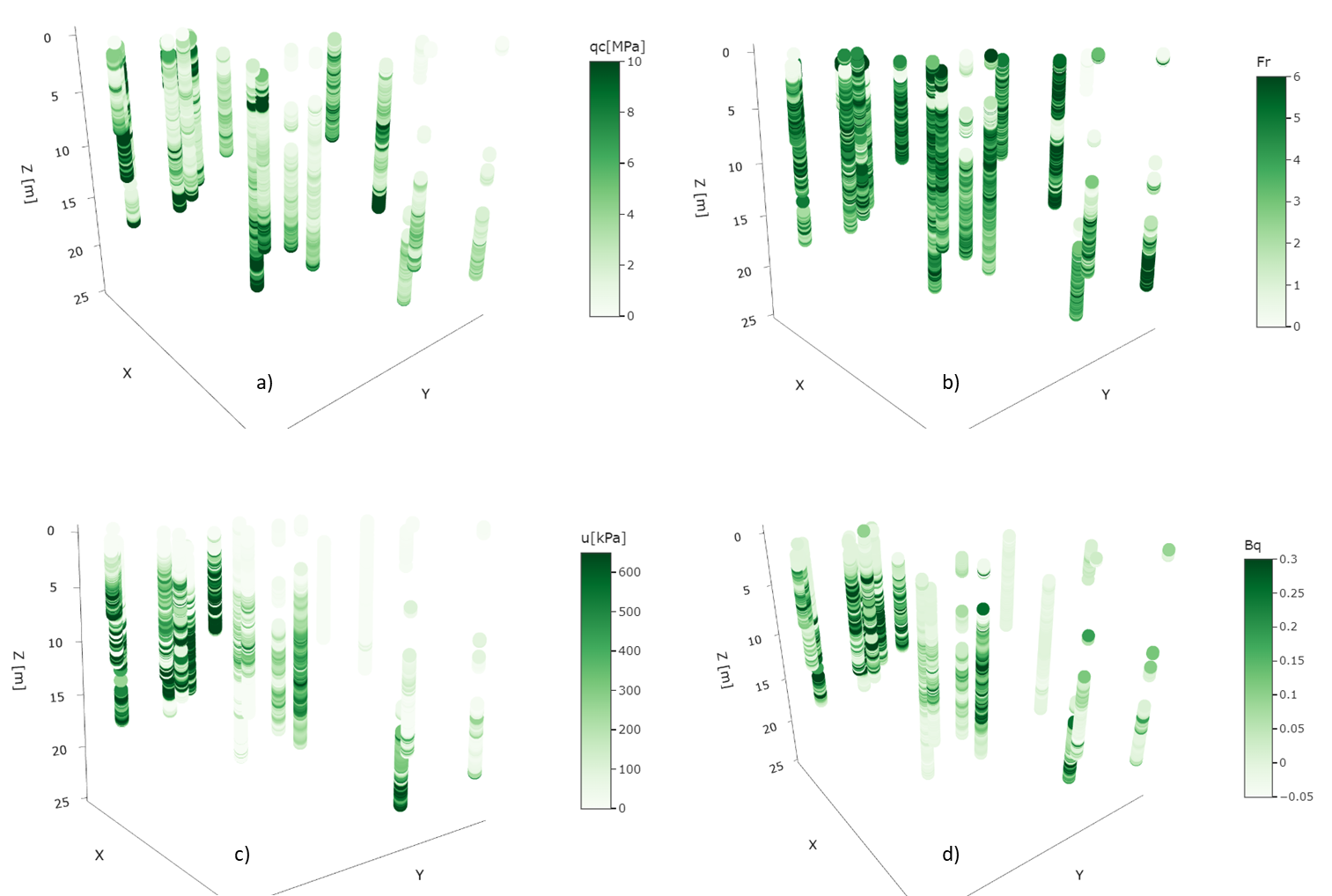
From Figure 9 e), it is possible to note that the existence of cluster 1 cannot be restricted to one layer or specific zone, since this material is spread without a clear pattern all over the study area. To check the matching between soil properties and to verify if cluster 1 is the very soft soil, the data were plotted in 3D. Figure 12 presents the data colored by a) the cone resistance, q_c, b) the friction ratio, F_r, c) the pore pressure during the cone penetration, u, and d) the pore pressure ratio, B_q. Comparing these figures with Figure 9 e), it is possible to conclude that cluster 1 has low cone resistance q_c, high pore pressure u (and consequently pore pressure ratio), and high friction ratio, F_r. The high pore pressure levels due to penetration corroborate the triaxial test results, showing that this is a soil that generates elevated excess pore pressure when subject to shear. On the other hand, cluster 0 (dark green) could be the soft soil, which also present low cone resistance and high friction ratio, but with lower pore pressure generated.

5. Conclusion

The interpretation and cluster analysis of the laboratory tests helped to understand the behavior of these soft and very soft residual soils when subject to shear, showing that the pore pressure parameter at failure (A_f) is the main difference between them. Knowing that these materials tend to differ in such manner increased the confidence in establishing B_q as the parameter on CPT that better distinguish them, as clearly observed in the comparison of adjacent SPT and CPT surveys. This is a very interesting outcome of this study, since tip resistance and friction ratio are much more commonly used for differentiating materials than B_q. Nevertheless, to confirm the results from the CPT cluster analysis, it would be valuable to have samples in-depth, since all laboratory samples were collected at the surface.

Although it was not possible to establish clear layers of very soft soil and the soft soil in CPT soundings, it was possible to see the location where the parameters indicate the possible existence of these soils. This lack of well-defined layers in this study should not be interpreted as an incapacity of the model or inadequacy of the laboratory tests or field surveys, but rather an intrinsic geological characteristic of these tropical residual soils, which show very complex weathering patterns and cannot be compared to the layered and better-defined depositions of sedimentary formations, for instance. It is safe to say that there is no guarantee that the very soft soil is restricted to a layer or a specific zone, and treating this problem in such way would not be the best approach, especially for ultimate state evaluation, such as a limit equilibrium analysis. A more realistic methodology could be to understand the spatial variability of the soil parameters and generate random fields, based on the scale of fluctuation observed.

References