1. Introduction

Hollow structural sections (HSS) possess several beneficial properties, such as a high strength-to-weight ratio, good compression, bending, and torsional resistance, which make HSS members suitable for various structural applications, e.g., columns, bracing members, cladding supports, and truss members [1-8]. Recently, HSS members have been researched as an alternative to wide flange moment resisting frame systems in low- or mid-rise structures in that using HSS-to-HSS moment resisting frame can limit the lateral bracing requirements and potentially reduce the seismic weight [1-8]. To understand the performances of HSS-to-HSS moment connections under seismic loading, several experimental and numerical studies have been conducted to evaluate the behaviors of HSS beam and connection details for cyclic loading [1-8]. Unreinforced HSS-to-HSS moment connections were investigated via finite element (FE) modelling by [6], in which HSS 355.6x355.6x15.9 was used for the column; a parametric study was conducted on several different connections with a beam width-to-column width ratio (β) ranging from 0.29 to 0.86; e.g., with an HSS 304.8x152.4x15.9 beam (β=0.43), and an HSS 304.8x203.2x15.9 beam (β=0.57) [6]. The research results showed that the normalized maximum moment of an HSS-to-HSS moment connection increased as the width ratio (β) increased, when the HSS-to-HSS connection was subjected to cyclic loading [6]. Fig. 1 shows the cyclic loading protocol used in [6].

For the unreinforced connections, it was reported that the plastic deformation was concentrated at the column face and the plastic moment capacity of the beam was not fully developed [6]. Fig. 2 depicts an example normalized moment vs. connection rotation (rad.) for the unreinforced connection with an HSS 355.6x355.6x15.9 column and an HSS 304.8x203.2x15.9 beam; note that the connection has a maximum normalized moment capacity of 0.28 [6].

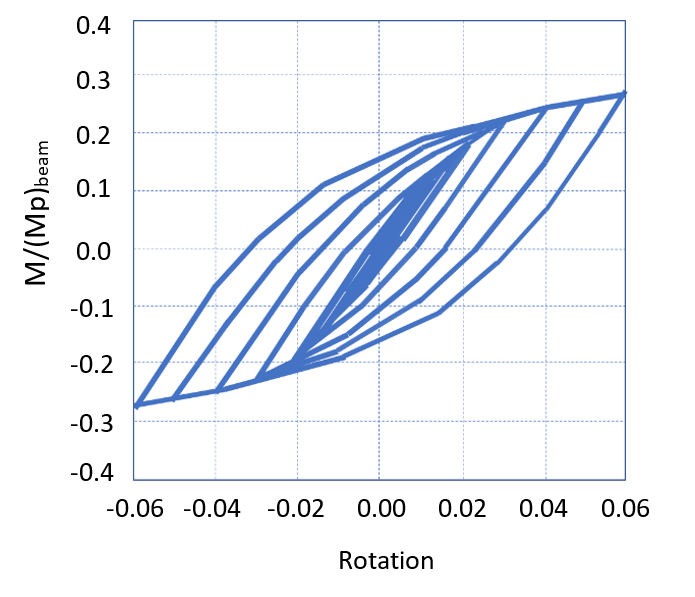
To achieve a more desirable connection for seismic application, reinforced HSS-to-HSS moment connections were investigated by [6], in which two different types of diaphragms (i.e., internal diaphragm and external diaphragm) were examined on connections with an HSS 355.6x355.6x15.9 column and an HSS 304.8x203.2x15.9 beam [6]. The studies indicated that the external diaphragm HSS-to-HSS connections were not able to develop full plastic moment capacity of the beam, whereas the internal diaphragm connections could achieve the full plastic moment capacity of the beam if adequate diaphragm thickness and diaphragm length were used [6]. It is worth noting that the unreinforced and reinforced HSS-to-HSS connections studied in [6] were of the concentric type of connection (i.e., the beam was centered and connected to the column) [6]. In real applications, eccentric HSS-to-HSS connections may be required in several situations, e.g., framing connected to stairwells, cantilevered canopies, and situations due to geometric or site limitations [9]. The connection eccentricity is measured by the perpendicular distance between the centreline of the column member and the centreline of the beam member, as shown in Fig. 3.

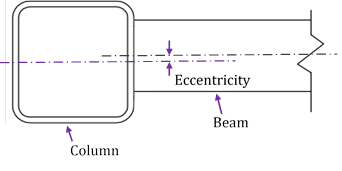
The presence of connection eccentricity might affect the load capacity of an HSS-to-HSS moment connection subjected to cyclic loading; however, such research has not been reported (to the best knowledge of the authors). Therefore, this paper aims to investigate the influence of connection eccentricity on the load capacity of HSS-to-HSS moment connections subjected to in-plane cyclic loading through FE simulations, as discussed in the next sections.

2. Finite Element Simulations

In this paper, two connection configurations from [6] were adopted for studies: Configuration 1 (Config. 1) has an HSS 355.6x355.6x15.9 column and an HSS 304.8x203.2x15.9 beam, whereas Configuration 2 (Config. 2) has an HSS 355.6x355.6x15.9 column and an HSS 304.8x152.4x15.9 beam; the beam width-to-column width ratios (β) for Configs. 1 and 2 are 0.57 and 0.43, respectively [6, 11]. The section corner radius was assumed as twice of the thickness of the member [5]. Both unreinforced and reinforced connections were investigated for each configuration. The cyclic bending behaviors of HSS-to-HSS connections were simulated by using ANSYS Workbench version 2021 R2 [12]. Solid elements were used to model the column and beam members in ANSYS in this study; note that shell elements were used for FE modelling in [6]. Fig. 4 illustrates an example FE model of the HSS-to-HSS beam-column moment connection (unreinforced) in ANSYS.

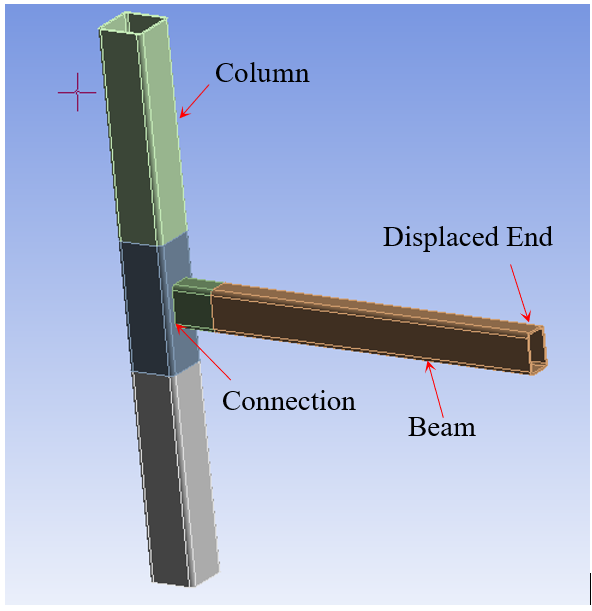
The details of FE simulation in [6] were referred to for the studies herein: the column has a length of 3962 mm, whereas the beam has a length of 2870 mm, for both configurations; non-linear FE analyses were used to determine the bending behavior of HSS-to-HSS moment connections under cyclic loading; the loading protocol from [6] (see Fig. 1) was employed to simulate the cyclic loading, which was applied to the displaced end of the beam; the other end of the beam (referred to as “fixed end”) was fixed to the column member by using the bonded type of connection [6]. Fixed supports were assumed and applied at both ends of the column as a boundary condition. Note that 1.3 cm square elements were used for the fixed end region of the beam, whereas 5.0 cm square elements were used for the displaced end region of the beam in [6,7]. A bilinear kinematic hardening law was used. The Young’s modulus and tangent modulus were assumed as of 200 GPa and 1.45 GPa, respectively; a value of 0.3 was assumed for the Poisson’s ratio of the steel [12]. The yield strength of the steel was assumed as of 450 MPa based on [3, 7]. A convergence study was performed to optimize the mesh size in the beam and column members; the FE model is divided into two regions: region 1 refers to the fixed end region of the beam member (310 mm) and the central region of the chord member (925 mm), whereas the remaining parts are referred to as region 2. The element mesh size of regions 2 is kept as 50 mm, whereas the mesh size at region 1 was reduced from 25 mm for convergence study; the maximum moment converged at a mesh size of 12 mm to 10 mm (moment difference is less than 1%). Thus, a mesh size of 12 mm was applied to region 1 to achieve both accuracy and computational efficiency. Fig. 5 shows the FE meshing of the moment connection model in ANSYS.

3. Finite Element Verification

To ensure the accuracy of FE simulation, the connection with an HSS 355.6x355.6x15.9 column and an HSS 304.8x203.2x15.9 beam from [6] was adopted for FE verification. By using the FE technique as aforementioned, the normalized moment vs. connection rotation (rad.) for the connection was obtained, as shown in Fig. 6.

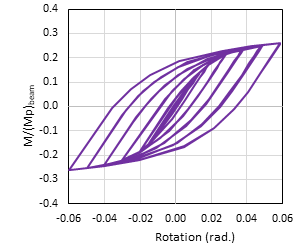
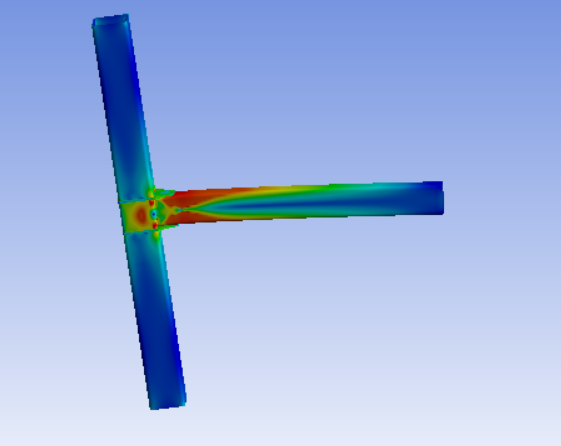
It can be observed that the hysteretic loops in Fig. 6 are similar to that in Fig. 2 (from [6]); the maximum normalized moment capacity obtained herein is 0.26, which is close to the value of 0.28 from [6]; the difference could be due to the different types of elements used in the FE simulations. It suggests that the FE simulation technique in this study can capture the bending behavior of HSS-to-HSS moment connections subjected to cyclic loading. In addition, von Mises stress distribution in the moment connection at 0.06 rad. rotation was obtained and shown in Fig. 7. It is evident that the plastic deformation was concentrated at the column face, which agrees well with the research findings from [6].

4. Effect of Connection Eccentricity

With the FE verification above, the FE simulation technique was used with confidence to examine the effect of connection eccentricity for HSS-to-HSS moment connections (unreinforced and reinforced types), as discussed next.

4. 1. Unreinforced connections

For the unreinforced HSS-to-HSS moment connections, two configurations were studied, namely, Config. 1 (β=0.57) and Config. 2 (β=0.43). A total of nine HSS-to-HSS moment connections were modelled for each configuration by varying the connection eccentricity. To explore the effects of connection eccentricity, the eccentricity of the connection was increased from 0 mm (i.e., without eccentricity) up to 40 mm by an increment of 5 mm from the centreline of the column member. Fig. 8 shows the maximum moment vs. connection eccentricity for Config. 1 and Config. 2. As can be seen, the maximum moment capacity in the unreinforced HSS-to-HSS connection increases as the connection eccentricity increases. For Config. 1, the maximum moment is 157.7 KN-m when the eccentricity is zero; when the eccentricity is 40 mm, the maximum moment capacity reaches 197.2 kN-m (an increase of 25% from zero eccentricity). A similar trend is observed for Config. 2: the maximum moment is 124.0 KN-m when the eccentricity is zero, whereas the maximum moment capacity reaches 138.5 kN-m (an increase of 11.7% from zero eccentricity) when the eccentricity is 40 mm. Note that, in this study, the width ratios (β) for Config. 1 and Config. 2 are 0.57 and 0.43, respectively. For a width ratio β ≤ 0.85, the column wall plastification occurs when the beam member is subjected to a bending moment [4]. When the connection eccentricity increases, the beam member gets shifted towards the sidewall of the column member where it should be stiffer [4], which explains the observation that a larger connection eccentricity yields a higher moment capacity. It can also be seen that the connection with a higher value of width ratio (β) demonstrates a higher moment capacity (at the same connection eccentricity); the reason could be that the beam member becomes wider as the value of β increases; thus, the beam gets closer to the sidewalls of the column which is stiffer [4], therefore resulting in a higher moment capacity of the connection. Additionally, it can be observed that Config. 1 has a higher rate of moment increase than Config. 2. Since Config. 1 has a higher β value than Config. 2, the beam in Config. 1 is closer to the sidewalls of the column; thus, with the increase of connection eccentricity, the effect of the column sidewall on the bending moment of Config. 1 connection may become more significant, which could explain why Config. 1 has a higher rate of moment increase.

For unreinforced HSS-to-HSS connections, since the moment capacity increases as connection eccentricity increases, an eccentric HSS-to-HSS moment connection can be conservatively designed as a concentric connection when the connection is subjected to in-plane cyclic loading.

4. 2. Reinforced connections

In [6], two different types of diaphragms were examined (i.e., internal diaphragm and external diaphragm), which showed that the internal diaphragm was more effective to achieve the full plastic moment capacity of the beam if adequate diaphragm thickness and diaphragm length were used [6]. Therefore, the internal diaphragm from [6] was adopted for studies in this paper to examine the effects of connection eccentricity for reinforced HSS-to-HSS moment connections. Fig. 9 shows an internal diaphragm HSS-to-HSS moment connection in ANSYS; note that the reinforced connection is made by adding the internal diaphragm to the beam and column of the unreinforced connection via complete joint penetration welds [6]. The bonded type of connection was used to connect the diaphragm to the members (beam and column) to simulate the welds [6]. Note that the FE simulation of the beam and column members in the reinforced connections were the same as the unreinforced connections above.

Fig. 10 shows the details of the internal diaphragm used in [6]. As reported by [6], a diaphragm length (ld) of 203.2mm and a thickness of 19.1mm was observed to be sufficient to develop the full plastic moment of the beam; the yield strength of 250 MPa was assumed for the diaphragm plate [6]; those details were adopted in the FE simulations in this paper. Also, Young’s modulus and tangent modulus were assumed as 200 GPa and 1.45 GPa, respectively, for the diaphragm steel [12].

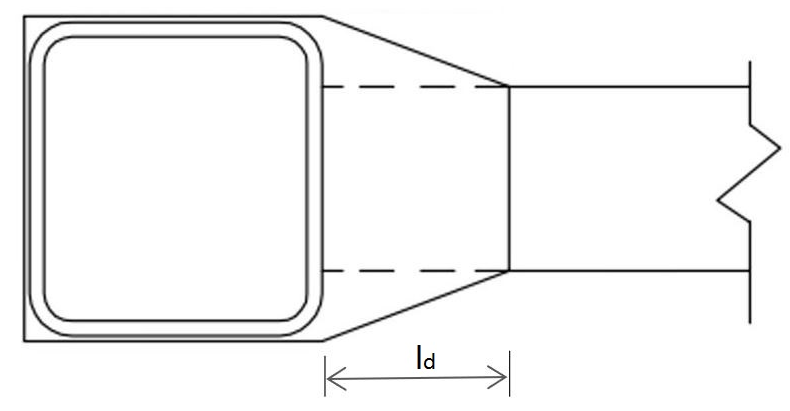
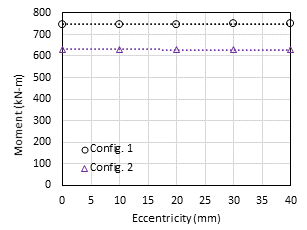
The same as the unreinforced connections, two configurations were studied, namely, Config. 1 (β=0.57) and Config. 2 (β=0.43), for the reinforced HSS-to-HSS connections. It is worth mentioning that Config. 1 and Config. 2 have the same column (i.e., HSS 355.6x355.6x15.9); however, Config. 1 has an HSS 304.8x203.2x15.9 beam, whereas Config. 2 has an HSS 304.8x152.4x15.9 beam. A total of five HSS-to-HSS moment connections were simulated for each configuration by varying the connection eccentricity; the eccentricity ranged from 0 mm (i.e., without eccentricity) to 40 mm by an increment of 10 mm. Fig. 11 shows the maximum moment vs. connection eccentricity for the reinforced HSS-to-HSS connections from FE simulations.

As can be seen, the moments stay almost the same when the connection eccentricity increases, for both Config. 1 and Config. 2 connections. It shows that the eccentricity has minimal effect on the maximum moment capacity of the reinforced HSS-to-HSS moment connection subjected to cyclic loading. Fig. 12 shows an example distribution of von Mises stresses in the internal diaphragm HSS-to-HSS moment connection at 0.06 rad. rotation. It can be observed that the plastic deformation was concentrated at the beam member, which agrees well with the research findings from [6].

Since the failure of the reinforced HSS-to-HSS moment connection was governed by the beam yielding, it explains why the moment capacity didn’t change with connection eccentricity (see Fig. 11). It can be said that the effect of connection eccentricity could be ignored when designing the moment capacity of an eccentric HSS-to-HSS moment connection (reinforced with internal diaphragm) subjected to in-plane cyclic loading.

5. Conclusion

In this paper, both unreinforced and reinforced HSS-to-HSS moment connections were numerically analysed via FE simulations. The effects of connection eccentricity were examined for two configurations with different beam width-to-column width ratios. Based on the research findings from this study, the following conclusions could be made for HSS-to-HSS connections subjected to in-plane cyclic loading, as follows:

• The moment capacity of an unreinforced HSS-to-HSS moment connection increases as the connection eccentricity increases, regardless of the width ratio.
• The moment capacity of a reinforced HSS-to-HSS moment connection stayed almost the same as the connection eccentricity increases, regardless of the width ratio.
• For both unreinforced and reinforced HSS-to-HSS moment connections, the presence of connection eccentricity should not be a concern as regards to the bending moment capacity of the connection when it is subjected to in-plane cyclic loading.
• For both unreinforced and reinforced HSS-to-HSS moment connections, the connection with a higher width ratio (β) demonstrates a higher moment capacity.

The research findings above provide valuable insight as to the effects of connection eccentricity on the moment capacity of HSS-to-HSS moment connections subjected to cyclic loading. Further research on other connection configurations is suggested and experimental studies are recommended.

References