Volume 7 - Year 2024- Pages 62-72
DOI: 10.11159/ijci.2024.007
Data-Fitted Shear Design Equations for EB FRP-RC Beams
H.H.N.D. Haggalla1, Sang-Wook Bae1
1Texas Tech University, Department of Civil, Environmental, and Construction Engineering,
2500 Broadway W, Lubbock, Texas, United States 79409
hhaggall@ttu.edu; sangwook.bae@ttu.edu
Abstract - Based on a data fitting method applied to 490 experimental test data that are publicly available in the literature, this study provides simplistic and straightforward equations to determine the shear capacity of FRP bonded-RC beams. Complete wrap, U-wrap, and side wrap schemes pertaining to Carbon Fiber Reinforced Polymer (CFRP) were analysed separately. Current design codes follow a customary approach where the nominal shear capacity is calculated by simply accumulating the shear contribution of concrete, transverse reinforcement, and FRP. The interaction between concrete, transverse reinforcement, and FRP is usually not taken into consideration. While the modulus of elasticity of FRP, transverse steel ratio, and FRP ratio all have an inverse interaction with the effective strain of FRP, the concrete compressive strength, longitudinal steel ratio, and the shear span-to-depth ratio are positively linked with the effective FRP strain. This investigation further showed that as transverse reinforcement is increased, the influence of FRP on shear contribution significantly decreases in the complete wrap scheme. ACI 440.2R-17, CSA S806-02 and its latest version CSA S806-12 are among the regularly used shear design codes in North America and they were used to compare the performance of the proposed equations. The obtained results show that the proposed equations predict the experimental results more accurately than ACI 440.2R-17, CSA S806-02, and CSA S806-12.
Keywords: Data fitting; Fiber reinforced polymers; Shear strength; RC beams; Curve fitting; Repair; Strengthening.
© Copyright 2024 Authors - This is an Open Access article published under the Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2023-10-05
Date Revised: 2024-05-29
Date Accepted: 2024-06-11
Date Published: 2024-07-02
1. Introduction
Over the last three decades, numerous analytical and experimental studies have been conducted to analyse the behavior of Reinforced Concrete (RC) beams strengthened in shear using externally bonded fiber-reinforced polymer (FRP) sheets. Due to the high strength-to-weight ratio, non-corrosive characteristics, design flexibility, and extended service life, FRP is gaining popularity over traditional strengthening techniques [1]. While shear behavior is extremely complex and unprecedented, shear failure is comparatively brittle and can lead to sudden, catastrophic failure [2]. Bonding of FRP reinforcement orthogonal to the shear crack plane has been revealed to provide higher load-carrying capacities [3]. This means that by aligning the external reinforcement so that the principal fiber direction is as parallel as possible to the maximum principal tensile stresses, shear strengthening of reinforced concrete members using fiber-reinforced polymer can be optimized. This alignment enhances the effectiveness of the FRP. In practical applications, such as beams under gravity loads or columns under seismic forces, the trajectories of maximum principal stress in shear-critical zones typically form an angle of about 45 degrees with the member axis. However, it is usually more practical to attach the external FRP reinforcement with the principal fiber direction perpendicular to the member axis. The idealization of FRP materials is similar to that of internal steel stirrups, suggesting that FRP enhances shear capacity by bearing tensile stresses at a relatively consistent strain. This strain could be the ultimate tensile strain of FRP, ϵfu, or a lower value. In this context, the external FRP is expected to stretch in the principal fiber direction to a strain level typically below the ultimate tensile strain, ϵfu. This strain is referred to as the effective strain ϵfe. When the effective strain is multiplied by the elastic modulus of FRP in the principal fiber direction, Ef, and the available FRP cross-sectional area, Afv, it represents the total force the FRP can sustain, Vfrp, at the point of shear failure of the element. Determining the effective FRP strain through rigorous analysis is extremely difficult, if not impossible. Nevertheless, understanding this concept is essential for comprehending how FRP materials enhance the shear capacity of RC members and for designing effective shear-strengthening strategies.
2. Related Work
With the growing demand for accurate prediction of shear, numerous analytical formulations have been derived to estimate the shear capacity of RC beams strengthened with FRP [1-2], [4-9]. However, most of these shear equations are semi-empirical and the experimental data available to study the shear behavior of RC structures strengthened using FRP is limited. Out of these, the prediction model developed by Triantafillou and Antonopoulos [4] is based on the assumption that FRP only carries normal stresses and therefore, develops an ultimate strain at the ultimate strength. This model is adopted by the current Eurocode. The model proposed by Khalifa [5] based on the FRP fiber orientation and an assumed crack pattern is the basis for the ACI 440.2R-17 [10]. In addition to that, the Canadian Standards Association (CSA-S806-02/CHBDC-2006 and CSA-S806-12) the Japan Society of Civil Engineers (JSCE 1997), the Norwegian Standard for Design of concrete structures (NS3473), and the Institution of Structural Engineers, UK (IStructE) have also developed design equations and guidelines for shear strengthening of RC structures using FRP. However, almost all these design equations are highly conservative which would potentially lead to costly and uneconomical designs. The National Cooperative Highway Research Program (NCHRP) report 678: Design of FRP systems for strengthening concrete girders in shear [11] summarizes all the design codes available.
Most previous studies have adopted non-linear statistical analyses on limited experimental results to develop various design equations for RC elements strengthened with FRP in shear. Matthys [12] has derived equations to estimate the effective FRP strain using the curve fitting method which can then be used to calculate the shear contribution of FRP. Colotti and Spadea [13] have developed equations using the truss model concept. Based on the equilibrium of forces in a cross-section of a beam at failure, Pellegrino and Moderna [14] have obtained a theoretical equation for effective FRP strain. Nehdi [15-16], and Kara [17] have taken a genetic algorithm approach whereas Hosseini and others [18-21] have adopted machine learning and neural networks. Anvari [22] has also used an evolutionary machine learning approach, named genetic expression programming. Shahnewaz and Alam [23] have proposed a genetic algorithm approach for predicting the shear strength of steel fiber RC (SFRC). These studies have proven to predict superior results as compared to the current design guidelines available. Furthermore, Lima and Barros [3], and Zhou [24] have carried out reliability-based design analyses of FRP shear-strengthened RC beams. Although there has been a lot of experimental and analytical research on this topic, it is still difficult to precisely determine the shear capacity of RC beams strengthened using FRP on their own. Therefore, the main objective of this study is to utilize a comprehensive database to develop a model that better predicts the shear strength of FRP-strengthened RC beams. Belarbi [25] has developed a database summarizing 50 experiments that led to 375 experimental results that have been done from 1992 to 2009. This is an extension of that work which was originally presented by Triantafillou and Antonopoulos [4] and later updated by Bousselham and Chaallal [26]. The database was developed by reviewing 68 experimental studies resulting in 744 experimental data that were available in the literature.
3. Shear Design Guidelines
The current design code available in the United States for the shear strengthening of RC beams using FRP is the ACI 440.2R-17 [10]. The nominal shear strength, Vn of a member strengthened with FRP multiplied by a strength reduction factor ϕ should exceed the required shear strength, Vu as per the Eqs. (1)-(2) given in ACI 318-19 [27]. The nominal shear strength is the accumulation of contributions from concrete, Vc, transverse steel reinforcement, Vs, and externally bonded, Vfrp. Three types of techniques are considered in applying externally bonded FRP in the design code, namely complete wrap, U-wrap, and side-wrap. Depending on the technique used, the shear contribution from FRP, Vfrp should further be multiplied by a strength reduction factor ψf= 0.95 for complete wrap members and ψf= 0.85 for U-wrap (3 sides) and side wrap (2 opposite sides) members. This method of direct addition or rather superposition of shear components is based on the truss model with a shear crack angle of 45 degrees. However, Colotti and Spadea [13] mentioned that this leads to an underestimation of the shear strength of RC beams:
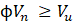
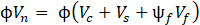
where, Vn is the nominal shear strength of the beam, Vu is the required shear strength. Eq.(3) given in ACI 440.2R-17 for calculating the shear contribution from FRP is adopted from Khalifa et al. [5].
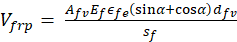
where, Vfrp is the shear contribution from FRP, Afv is the cross-section area of FRP, Ef is the modulus of elasticity of FRP, ϵfe is the FRP effective strain, α is the angle of orientation of FRP, dfv and sf are the effective depth and spacing of FRP, respectively. The most critical variable in estimating the shear contribution from FRP, Vfrp is the effective strain, ϵfe. The failure mode of both the FRP system and the strengthened RC member determines the maximum strain that can be achieved in the FRP system at the nominal strength, which is known as the effective strain in FRP laminates, ϵfe. The effective strain, ϵfe is typically lower than the ultimate strain ϵfu, because of strain changes along the shear fracture, local debonding on either side along the shear crack, or potential bond failure. Generally, the experimental values obtained for ϵfe are only approximate. On the other hand, the interaction of the effective strain, ϵfe with concrete strength, ![]() , and transverse reinforcement ratio,
ρs cannot be neglected. Furthermore, when calculating the shear contribution from the transverse reinforcement, it is assumed that they have yielded; however, in reality, this may not always be the case when additional FRP is applied, and the beam fails prematurely due to the debonding of FRP. The equations and the method provided in the ACI 440.2R-17 overestimate the shear contribution from transverse reinforcement, do not consider the interaction between the concrete, steel, and FRP, and therefore, underestimate the shear contribution from FRP [14].
, and transverse reinforcement ratio,
ρs cannot be neglected. Furthermore, when calculating the shear contribution from the transverse reinforcement, it is assumed that they have yielded; however, in reality, this may not always be the case when additional FRP is applied, and the beam fails prematurely due to the debonding of FRP. The equations and the method provided in the ACI 440.2R-17 overestimate the shear contribution from transverse reinforcement, do not consider the interaction between the concrete, steel, and FRP, and therefore, underestimate the shear contribution from FRP [14].
4. Database Used for this Study
4. 1. Formation of the Database
The most significant aspect of this study is the database that was created to capture data on the shear strengthening of RC beams using FRP spanning from 1992 to 2022. This resulted in 744 test data. For each test data, experimental details were recorded under 25 categories: beam shape, span-to-depth ratio, FRP type, compressive strength of concrete, type of compressive strength test (cylinder/cube), width of the beam, the effective depth of the beam, area of longitudinal reinforcement, yield strength of transverse reinforcement, area of transverse reinforcement, spacing, and transverse reinforcement ratio. In relation to FRP, width, thickness, effective depth, number of wraps, spacing, reinforcement ratio, angle of primary fiber direction, modulus of elasticity, tensile strength, and wrapping scheme were recorded. In addition to that, the ultimate shear force at failure, the contribution of FRP to the overall shear strength, and the failure mode of each beam were recorded.
As in any data collection process, biases can be expected here as well. Therefore, steps were taken to refine the database. There were a few potential sources of biases in the dataset. To ensure that the dataset is free from sampling bias, beams that have FRP stirrups or FRP bars as longitudinal reinforcement were omitted as this study is only focused on externally bonded FRP for shear strengthening. Prestressed and post-tensioned beams were not considered. In addition, beams with circular holes/openings and inverted T-beams were also removed. Beams that were constructed with fiber-mixed concrete and beams with FRP or mechanical anchorage were also omitted. Experiments that were carried out with impact loading in place of static loading were also removed. All these test data were underrepresented compared to the complete dataset. Moreover, in certain literature, key experimental data that was of interest in this study have not been recorded. In such cases, attempts were made to calculate missing data from the data that is already available. However, in cases where missing data were not able to be retrieved by any method, such test data were removed.
After a thorough process of refining the raw data, the final dataset comprised 490 test data. Out of these 490-test data, 119 were T-beams and the rest were rectangular beams. The shear strength of 333 beams was improved using FRP. The number of beams shear strengthened with AFRP, CFRP, and GFRP were 25, 285, and 23, respectively. The number of beams that were completely wrapped, U-wrapped, and side-wrapped were 66, 185, and 82, respectively, while 157 were control beams. Beams that were wrapped with novel techniques were not included in this study as they were underrepresented. Based on the analysis of previous literature, it can be concluded that this is one of the most comprehensive databases available to date. Over a period from 1992 to 2022, fewer than 1000 experimental results have been documented, highlighting a significant gap and underscoring the necessity for more experimental studies in this area.
4. 2. Significance of the Database
Out of the 490-test data, 333 test data provided information on beams strengthened in shear with FRP. Three types of FRP were considered namely, Aramid, Glass, and Carbon. However, 285-test data pertaining to CFRP were only considered in this study. The data was further divided, depending on the wrapping scheme: completely wrapped, U-wrapped, and side-wrapped. Before performing detailed analyses, the data was further divided based on the provision of transverse reinforcement. A detailed overview of each set of data with FRP for shear strengthening is shown in Table 1.
The descriptive statistics of each category of data are presented in Table 2. Here, fc' is the concrete compressive strength, tf is the thickness of FRP, wf is the width of FRP, df is the effective depth of FRP, sf is the spacing of FRP, Efrp is the modulus of elasticity of FRP, ffu is the tensile strength of FRP, ρf is the reinforcement ratio of FRP, εfe is the effective strain of FRP, bw is the width of the concrete beam, def is the effective depth of the beam, ρs is the longitudinal reinforcement ratio, a/d is the shear span to effective depth ratio, fyv is the yield strength of transverse reinforcement, Av is the area of transverse reinforcement, sv is the transverse reinforcement spacing, sf is the transverse reinforcement ratio, α is the angle of primary fiber direction, Vu is the ultimate shear force, and Vfrp is the shear contribution from FRP. Eq. (3) indicates that determining the effective FRP strain is crucial for predicting the shear contribution of the external FRP reinforcement. The crack opening along the shear crack, local FRP debonding on both sides of the shear crack, the development length of FRP, which depends on the bond at the FRP-concrete interface, and the axial rigidity of FRP all play a role in the estimation of this strain [16].
Table 1. Detailed database of shear strengthening using FRP
|
Beam shape |
Wrapping scheme |
Provision of stirrups |
Failure modes |
|
Rectangular (223) |
C (40) |
WS (27) |
R (16) and O (11) |
|
W/OS (13) |
D (1), R (5), and O (7) |
||
|
U (112) |
WS (57) |
D (54) and O (3) |
|
|
W/OS (55) |
D (30), R (8), and O (17) |
||
|
S (71) |
WS (40) |
D (29) and O (11) |
|
|
W/OS (31) |
D (28), R (1), and O (2) |
||
|
T-beam (62) |
C (0) |
WS (0) |
- |
|
W/OS (0) |
- |
||
|
U (60) |
WS (38) |
D (11), R (11), and O (16) |
|
|
W/OS (22) |
D (10), R (7), and O (5) |
||
|
S (2) |
WS (1) |
D (1) |
|
|
W/OS (1) |
D (1) |
Note 2: WS=with stirrup, W/OS = without stirrup
Note 3: D=Debonding, R=Rupture, and O=Shear and other modes of failure
Note 4: The number in parenthesis represents the number of beams in each category
The effective strain, ϵfe is therefore calibrated using a function of ![]() which indicated a power function as shown in Figure 1 (inclusive of first and third quartiles). Initially, a correlation analysis was run for the full dataset which indicated that out of all 3 wrapping schemes considered, complete wrapping is the most efficient, while the two-side wrapping is the least efficient. Therefore, it was decided to analyse complete wrap, U-wrap, and side-wrap schemes separately. This analysis further indicated an inverse correlation between the shear contribution from FRP and the transverse steel ratio, which further supports the fact that as the transverse reinforcement is increased, the effect of FRP on shear contribution becomes less [15]. ACI 318-19 recommends that concentrated loads should be placed within a distance of 2h from the face of the support, given that h is the beam height. Consequently, the lower bound for the shear span-to-depth ratio, a/d, is taken as 2, although in practice, this ratio might be slightly higher because the effective beam depth, def, is usually somewhat less than the overall beam height, h. This distinguishes between deep beams (a/d<2) and regular beams (a/d≥2). There is a greater increase in shear resistance due to FRP for slender beams compared to deep beams, likely due to the arch action exhibited by deep beams. Therefore, the shear contribution of externally bonded FRP is less significant for deep beams than for slender beams, indicating that the shear span-to-depth ratio, a/d, is positively correlated with the effective FRP strain. Similarly, the concrete compressive strength, fc', and the longitudinal reinforcement, ρs, due to dowel action also exhibit a positive trend with respect to effective FRP strain. Conversely, for transverse reinforcement, ρv, this trend is negatively correlated. Similar behavior has been observed by Lima and Barros [3] and Collins [28] for regular beams. In particular, the dataset of beams strengthened using the U-wrap scheme, which was also reinforced with stirrups, was used to study the correlation in depth between the variables in consideration concerning the effective strain, ϵfe as it is the largest sample data set available.
which indicated a power function as shown in Figure 1 (inclusive of first and third quartiles). Initially, a correlation analysis was run for the full dataset which indicated that out of all 3 wrapping schemes considered, complete wrapping is the most efficient, while the two-side wrapping is the least efficient. Therefore, it was decided to analyse complete wrap, U-wrap, and side-wrap schemes separately. This analysis further indicated an inverse correlation between the shear contribution from FRP and the transverse steel ratio, which further supports the fact that as the transverse reinforcement is increased, the effect of FRP on shear contribution becomes less [15]. ACI 318-19 recommends that concentrated loads should be placed within a distance of 2h from the face of the support, given that h is the beam height. Consequently, the lower bound for the shear span-to-depth ratio, a/d, is taken as 2, although in practice, this ratio might be slightly higher because the effective beam depth, def, is usually somewhat less than the overall beam height, h. This distinguishes between deep beams (a/d<2) and regular beams (a/d≥2). There is a greater increase in shear resistance due to FRP for slender beams compared to deep beams, likely due to the arch action exhibited by deep beams. Therefore, the shear contribution of externally bonded FRP is less significant for deep beams than for slender beams, indicating that the shear span-to-depth ratio, a/d, is positively correlated with the effective FRP strain. Similarly, the concrete compressive strength, fc', and the longitudinal reinforcement, ρs, due to dowel action also exhibit a positive trend with respect to effective FRP strain. Conversely, for transverse reinforcement, ρv, this trend is negatively correlated. Similar behavior has been observed by Lima and Barros [3] and Collins [28] for regular beams. In particular, the dataset of beams strengthened using the U-wrap scheme, which was also reinforced with stirrups, was used to study the correlation in depth between the variables in consideration concerning the effective strain, ϵfe as it is the largest sample data set available.
Table 2. Descriptive statistics of the input parameters
|
Parameter |
Min. |
Max. |
Mean |
|
fc' [MPa] |
11 |
57 |
31 |
|
tf [mm] |
0.05 |
25 |
0.46 |
|
wf [mm] |
1 |
800 |
98.55 |
|
df [mm] |
85 |
1028 |
289 |
|
sf [mm] |
1 |
800 |
141.73 |
|
Efrp [GPa] |
5.3 |
390 |
196.3 |
|
ffu [MPa] |
106 |
4902 |
3152 |
|
ρf |
0.000138 |
0.17 |
0.0053 |
|
ϵfe [mm/mm] |
-0.00013 |
0.049 |
0.0053 |
|
bw [mm] |
63.5 |
600 |
181 |
|
def [mm] |
85 |
1028 |
317 |
| ρs |
0 |
18.72 |
3.03 |
|
fyv [MPa] |
0 |
653 |
240 |
|
Av [mm2] |
0 |
142 |
40 |
|
sv [mm] |
0 |
800 |
148 |
| ρv |
0 |
0.011 |
0.0013 |
|
α |
0 |
90 |
80 |
|
Vu [kN] |
18.8 |
1584.5 |
226.1 |
|
Vfrp [kN] |
-0.98 |
492.9 |
74.5 |
The parameters which had the most significant correlation with the effective strain, ϵfe of FRP are shown in the correlation plot in Figure 2. The model error of current ACI 440.2R-17 concerning the experimental results obtained in terms of the shear contribution from FRP was measured using ![]() which resulted in 1.5 for rectangular beams and 0.66 for T-beams respectively. This suggests that the ACI 440.2R-17 underestimates the shear contribution of FRP, Vfrp, for rectangular beams and overestimates for T-beams. In general, the difference between Vfrp,exp (the experimentally measured shear strength) and Vfrp,calc (the calculated shear strength) highlights the accuracy and reliability of the ACI 440.2R-17 used to predict the shear strength of FRP-reinforced beams. An overestimation occurs when Vfrp,calc is significantly higher than Vfrp,exp indicating that ACI 440.2R-17 predicts a higher shear strength than what is observed experimentally. This could lead to unsafe designs, as the actual strength of the beams would be lower than predicted, potentially resulting in structural failures. In contrast, underestimation happens when Vfrp,exp is considerably lower than Vfrp,exp, meaning ACI 440.2R-17 predicts a lower shear strength than what is measured experimentally. While this conservative approach is safer, it may result in overdesign, causing unnecessary use of materials and increased costs. Understanding and minimizing these differences is crucial for refining the design codes to ensure that calculated shear strength values closely match experimental results, improving the safety, reliability, and cost-effectiveness of FRP-reinforced beam designs.
which resulted in 1.5 for rectangular beams and 0.66 for T-beams respectively. This suggests that the ACI 440.2R-17 underestimates the shear contribution of FRP, Vfrp, for rectangular beams and overestimates for T-beams. In general, the difference between Vfrp,exp (the experimentally measured shear strength) and Vfrp,calc (the calculated shear strength) highlights the accuracy and reliability of the ACI 440.2R-17 used to predict the shear strength of FRP-reinforced beams. An overestimation occurs when Vfrp,calc is significantly higher than Vfrp,exp indicating that ACI 440.2R-17 predicts a higher shear strength than what is observed experimentally. This could lead to unsafe designs, as the actual strength of the beams would be lower than predicted, potentially resulting in structural failures. In contrast, underestimation happens when Vfrp,exp is considerably lower than Vfrp,exp, meaning ACI 440.2R-17 predicts a lower shear strength than what is measured experimentally. While this conservative approach is safer, it may result in overdesign, causing unnecessary use of materials and increased costs. Understanding and minimizing these differences is crucial for refining the design codes to ensure that calculated shear strength values closely match experimental results, improving the safety, reliability, and cost-effectiveness of FRP-reinforced beam designs.
Further insights into the model error fluctuation are depicted in Figure 3, revealing the need for substantial improvement in ACI 440.2R-17 guidelines. The analysis shows that the maximum overestimation reaches about 80%, while the maximum underestimation is approximately 50%. These notable discrepancies reveal that the estimated values in ACI 440.2R-17 do not closely match the experimental values, failing to fall within a range of at least ±20%. Such large errors highlight critical areas where the ACI 440.2R-17 significantly overestimates or underestimates the actual shear strength of FRP-reinforced beams. This emphasizes the need to enhance ACI guidelines for more accurate shear strength predictions, ensuring safer and cost-effective structural designs.
5. Proposed Model
The correlation analysis in Figure 2 revealed that the compressive strength of concrete, ![]() , has a positive correlation with effective strain, ϵfe while longitudinal steel ratio, ρs, transverse steel ratio, ρv, FRP ratio, ρf, and modulus of elasticity of FRP, Ef all have a negative correlation with ϵfe. With the scatter plot obtained for effective strain, ϵfe along with the variables in consideration that indicated a power function (see Figure 1), it was evident that the data calls for a non-linear regression analysis. With the influence of the studies done by Pellegrino and Modena [14] and Nehdi and Nikopour [16], since the distribution of the data was generally known, it was decided to derive a custom equation based on experimental data fitting in the form of Eq. (4) to find the coefficients that provide the best fit. The coefficients C1 and C2 are unknown. An exponential curve fitting method in the commercially available software MATLAB 2023 version was used for this purpose. A similar approach was taken for the side wrapping and complete wrapping schemes as well. For beams without transverse reinforcement, Eq. (5) was considered:
, has a positive correlation with effective strain, ϵfe while longitudinal steel ratio, ρs, transverse steel ratio, ρv, FRP ratio, ρf, and modulus of elasticity of FRP, Ef all have a negative correlation with ϵfe. With the scatter plot obtained for effective strain, ϵfe along with the variables in consideration that indicated a power function (see Figure 1), it was evident that the data calls for a non-linear regression analysis. With the influence of the studies done by Pellegrino and Modena [14] and Nehdi and Nikopour [16], since the distribution of the data was generally known, it was decided to derive a custom equation based on experimental data fitting in the form of Eq. (4) to find the coefficients that provide the best fit. The coefficients C1 and C2 are unknown. An exponential curve fitting method in the commercially available software MATLAB 2023 version was used for this purpose. A similar approach was taken for the side wrapping and complete wrapping schemes as well. For beams without transverse reinforcement, Eq. (5) was considered:

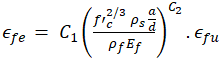
While the preceding formulae for effective strain, ϵfe do not explicitly consider the strain distribution along the shear fracture and the FRP bond behavior, they have the advantage of avoiding complicated expressions that would otherwise be provided by methods such as genetic algorithms or machine learning. The results for ϵfe obtained from the above equations were used to calculate the shear contribution from FRP as given in Eq. (6).
Moreover, it is interesting to note the dependency of the effective strain of FRP, ϵfe on transverse steel ratio, longitudinal steel ratio, and the shear span-to-depth ratio and not just on the stiffness of FRP, ρf Ef (refer to Figure 2). This prevails the importance of considering the interaction of FRP with concrete, longitudinal, and transverse reinforcement when investigating the behavior of shear. The estimated new effective strain values were then used to calculate the shear contribution of FRP as shown in Eq. (6) where ϵfe* is the estimated effective FRP strain.
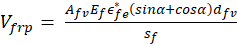
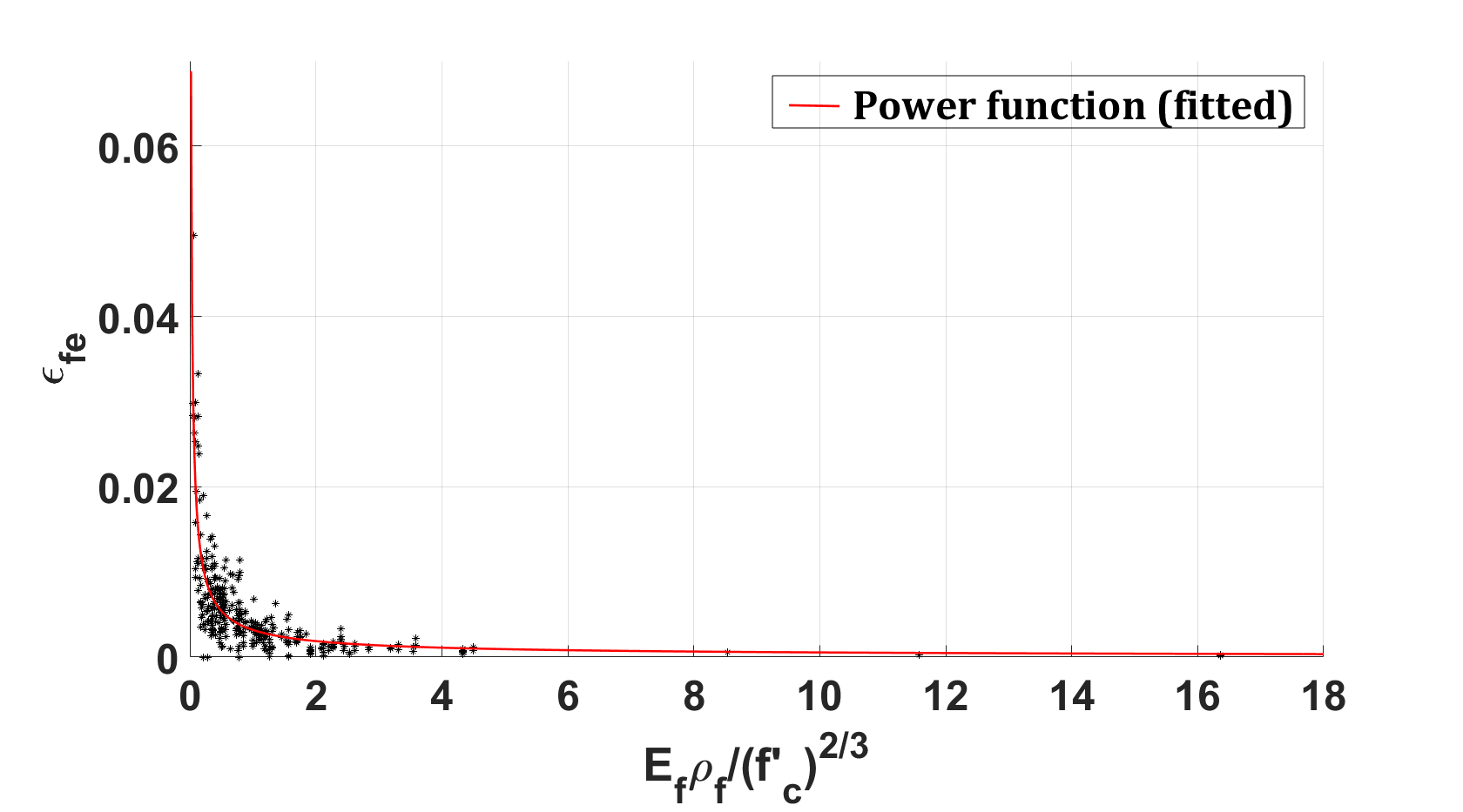 Figure 1. Power function variation of ϵfe vs.
Figure 1. Power function variation of ϵfe vs. 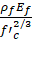
6. Results and Discussion
Since the database contained different types of FRP sheets, initially, the ratio R = ϵfe/ϵfu was considered to examine the percentage of effective strain, ϵfe with respect to the ultimate strain of FRP, ϵfu which should ideally be ≤ 1, assuming any unrealistic data has been omitted already during the database refining process. The resulting ratios obtained are shown in Table 3. For both U-wrap and side-wrap schemes, the results indicate that beams with stirrups have reached a similar effective strain compared to beams without stirrups. However, for the complete wrap scheme, beams without stirrups have reached a higher effective strain as compared to beams with stirrups.
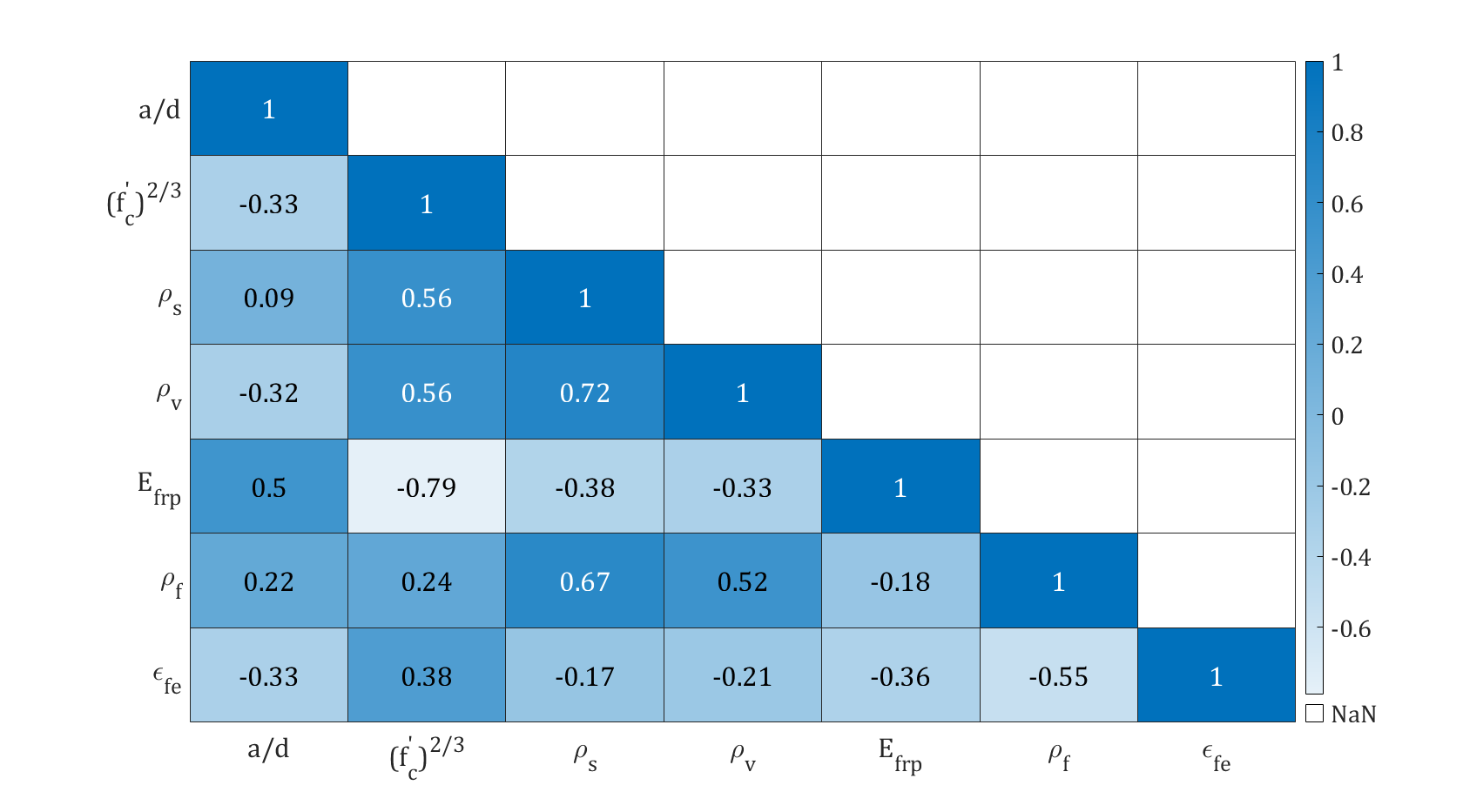 Figure 2. Correlation between input parameters in beams shear strengthened using CFRP (U-wrap)
Figure 2. Correlation between input parameters in beams shear strengthened using CFRP (U-wrap) Table 3. Values for R, C1, and C2 obtained to estimate ϵfe
|
R = |
C1 |
C2 |
|||
|
Rectangular beams |
C |
WS |
51.3 % |
0.24 |
0.12 |
|
W/OS |
60.8 % |
0.43 |
0.67 |
||
|
U |
WS |
29.7 % |
0.02 |
0.45 |
|
|
W/OS |
29.7 % |
0.33 |
0.30 |
||
|
S |
WS |
15.5 % |
0.0085 |
0.55 |
|
|
W/OS |
15.3 % |
0.48 |
0.58 |
||
Note 2: WS=with stirrup, W/OS = without stirrup
As mentioned before, this provides more evidence that the impact of FRP on shear contribution decreases as transverse reinforcement is increased. This could be due to the fact that the complete wrap scheme has a higher force transfer zone on either side of the shear crack, which is the development length of FRP and, therefore, precedes stirrups in shear resistance. Moreover, complete wrapping schemes indicate higher effective strain, ϵfe overall. It is apparent that FRP wrapping configuration significantly influences the shear strengthening and closed-shaped/complete wrapping schemes are likely to provide higher failure loads. The coefficients C1 and C2 found for each CFRP-wrapping scheme are given in Table 3. It is important to note that the results obtained from this analysis are based on U.S. customary units. The available data on AFRP and GFRP were insufficient to perform the analyses and therefore, they were not considered. The final strain level in the FRP sheets corresponds to the coefficients C1 and C2. For beams with transverse reinforcement strengthened using CFRP, evidently, the complete wrap scheme without stirrups has the highest C1 and the side wrap scheme with stirrups has the lowest. Whereas the complete wrap scheme without stirrups has the highest C2 and the complete wrap scheme with stirrups has the lowest. This means that the complete wrap scheme without stirrups reaches closer to its ultimate strain therefore, ultimate capacity provides better efficiency compared to the U-wrap and side wrap bond applications. However, this is not the case for beams without transverse reinforcement strengthened using CFRP. Regardless of the provision of stirrups, both U-wrap and side wrap schemes tend to exhibit similar efficiency. However, the effective strain percentage of the U-wrap scheme is as twice much as the side wrap scheme. On average, the proposed model for ϵfe well agrees with the experimental results for all the wrapping schemes. With the new estimated effective FRP strains, the new shear contribution from FRP, Vfrp was calculated and compared against the experimental values, which indicated a similar variation as the estimated effective FRP strain,ϵfe .
The ability of the stirrups to yield or not, however, could not be determined because the shear contribution from transverse reinforcement was not available for all test data. This prevented a comparison of the experimental and estimated ultimate shear forces, which are the result of the sum of the shear contributions from the concrete, transverse reinforcement, and FRP.
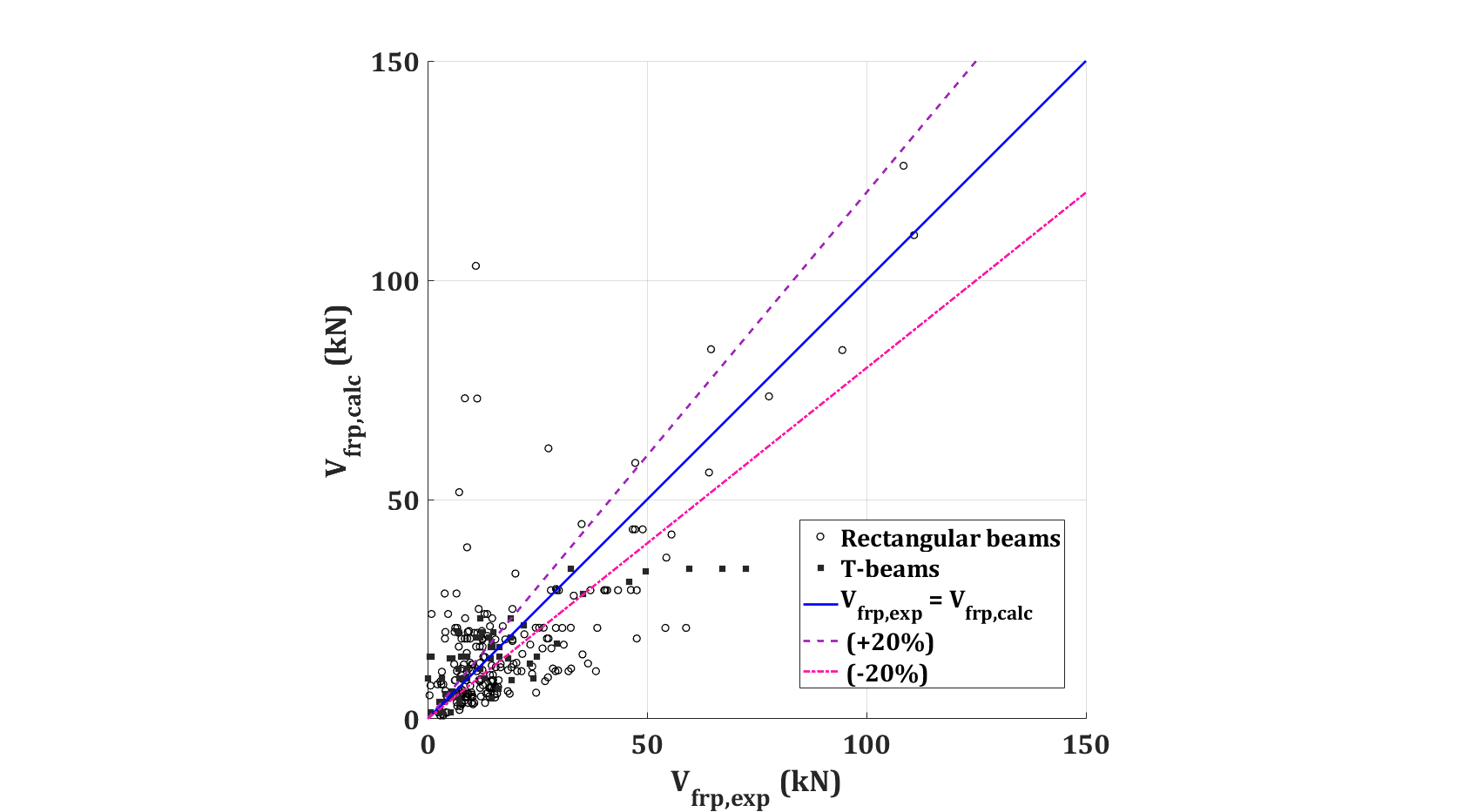
Furthermore, the results were compared against the design codes available to investigate the applicability of the proposed equations (see Table 4). For each wrapping scheme, the mean, and the standard deviation between the ratio of ![]() were calculated and tabulated in Table 4. As far as design codes are concerned, the ACI 440.2R-17, CSA-S806-02 [29], and CSA-S806-12 [30] were considered in this analysis. These codes don’t consider the interaction between RC, transverse reinforcement, and FRP when estimating the shear contribution of FRP. Compared to the ACI 440.2R-17, the proposed equations based on data fitting provide comparatively better results. A detailed summary of the design equations for ACI 440.2R-17 and CSA-S806-02 are shown in Table 5. The deviation of the results is comparatively lower in the proposed method when compared to ACI 440.2R-17.
were calculated and tabulated in Table 4. As far as design codes are concerned, the ACI 440.2R-17, CSA-S806-02 [29], and CSA-S806-12 [30] were considered in this analysis. These codes don’t consider the interaction between RC, transverse reinforcement, and FRP when estimating the shear contribution of FRP. Compared to the ACI 440.2R-17, the proposed equations based on data fitting provide comparatively better results. A detailed summary of the design equations for ACI 440.2R-17 and CSA-S806-02 are shown in Table 5. The deviation of the results is comparatively lower in the proposed method when compared to ACI 440.2R-17.
Table 4. Performance considerations for the shear design equations
|
|
Complete wrap |
U-wrap |
Side wrap |
||||||||||
|
With transverse reinforcement |
Without transverse reinforcement |
With transverse reinforcement |
Without transverse reinforcement |
With transverse reinforcement |
Without transverse reinforcement |
||||||||
|
Method |
Mean |
SD |
Mean |
SD |
Mean |
SD |
Mean |
SD |
Mean |
SD |
Mean |
SD |
|
|
Proposed Equations |
1.00 |
0.40 |
1.00 |
0.52 |
0.97 |
0.38 |
1.01 |
0.45 |
0.95 |
0.58 |
1.01 |
0.59 |
|
|
ACI 440.2R-17 |
2.01 |
0.86 |
1.65 |
0.80 |
1.29 |
0.60 |
1.20 |
0.93 |
0.98 |
0.97 |
-0.06 |
4.78 |
|
|
CSA S806-02 |
1.63 |
1.21 |
1.66 |
0.86 |
0.66 |
0.47 |
0.82 |
0.47 |
0.92 |
0.98 |
0.45 |
0.35 |
|
|
CSA S806-12 |
2.40 |
1.01 |
3.94 |
3.05 |
1.07 |
0.73 |
2.16 |
1.20 |
0.64 |
0.73 |
0.96 |
0.76 |
|
Evidently, the side wrap scheme should be further investigated, and the design equations provided in the ACI 440.2R-17 and CSA-S806 ought to be revised. Both ACI 440.2R-17 and CSA-S806-02 underestimate the contribution from FRP in the complete wrap scheme. Meanwhile, the CSA S806-12 standard significantly underestimates the shear contribution of FRP for complete and U-wrap schemes, while it overestimates the shear contribution in the side wrap scheme. For the side wrap scheme, all three codes overestimate the results with a higher scatter of results for beams with transverse reinforcement. Perceptibly, beams shear reinforced using the side wrap scheme need much more investigation. In the U-wrap scheme, ACI 440.2R-17 underestimates results by about 20%-30%, and CSA-S806-02 overestimates this by a similar percentage. Meanwhile CSA-S806-12 underestimates results by about 10%-15%.



5. Conclusion
Based on the data fitting method, this study developed shear design equations for FRP-RC beams with and without FRP stirrups. Results for shear strength computed using the suggested equations are in good agreement with the experimental findings in the database considered. When compared to the majority of research, which has developed complex equations utilizing various statistical methodologies, such as machine learning, etc., these equations are significantly more straightforward and simplistic. Conclusively, the following summary can be made:
- Through this study, an extensive repository containing 490 test data relevant to RC beams shear strengthened utilizing FRP was created. This database underwent a rigorous refining process. When compared to preceding publications, this could be regarded as one of the most comprehensive databases yet created.
- The two-sided wrapping is the least efficient, according to the correlation study carried out using the database, while the complete wrapping is the most efficient.
- This analysis also revealed an inverse relationship between the shear contribution from FRP and the transverse steel ratio, further demonstrating that the effect of FRP on shear contribution decreases as transverse reinforcement is increased. Evidently, the completely wrapped beams without stirrups showed higher effective strain than beams with stirrups. This may be taken into account given that transverse reinforcement is preceded in shear resistance by the complete wrap FRP-strengthening design, since it has a higher force transfer zone on each side of the shear crack. Complete wrapping methods, however, generally show higher effective strain and are hence, likely to produce higher failure loads.
- To optimize the equations for the shear design of FRP-RC beams, the curve fitting approach can be a useful tool. The results obtained from the analysis are in good agreement with experimental results.
- The suggested equation shows how the FRP effective strain, ϵfe is dependent on the compressive strength of the RC, the axial stiffness of FRP, the transverse reinforcement, and the longitudinal reinforcement. however, the current design codes do not consider this. When assessing the performance of RC beams shear enhanced using FRP, it is crucial to take this interaction between the parts into account.
- The current ACI 440.2R-17 code exhibited subpar performance compared to the equations proposed in this study developed using the curve fitting method. However, the proposed technique should be further examined for the side wrap scheme in beams with transverse reinforcement because it greatly increased the standard deviation of the results for the predicted shear contribution of FRP. The Canadian standards (CSA-S806-02 & CSA-S806-12) investigated in this study behave in a similar manner.
- It is recommended that AFRP and GFRP be added to the database of experimental findings for shear strengthening utilizing CFRP in order to conduct a more thorough analysis and produce optimized equations.
References
[1] J. F. Chen and J. G. Teng, 'Shear capacity of FRP-strengthened RC beams: FRP debonding', Construction and Building Materials, vol. 17, no. 1, pp. 27-41, Feb. 2003, doi: 10.1016/S0950-0618(02)00091-0.
View Article
[2] A. Khalifa and A. Nanni, 'Rehabilitation of rectangular simply supported RC beams with shear deficiencies using CFRP composites', Construction and Building Materials, vol. 16, no. 3, pp. 135-146, Apr. 2002, doi: 10.1016/S0950-0618(02)00002-8.
View Article
[3] J.L.T. Lima and J.A.O. Barros, "Design Models for Shear Strengthening of Reinforced Concrete Beams with Externally Bonded FRP Composites: A Statistical vs Reliability Approach," presented at the 8th International Symposium on Fiber-Reinforced Polymer Reinforcement for Concrete Structures (FRPRCS-8), University of Patras, Patras, Greece, July 16-18, 2007.
[4] T. C. Triantafillou and C. P. Antonopoulos, 'Design of concrete flexural members strengthened in shear with FRP', Journal of Composites for Construction, vol. 4, no. 4, pp. 198-205, 2000, doi: 10.1061/(ASCE)1090-0268(2000)4:4(198).
View Article
[5] A. Khalifa, W. J. Gold, A. Nanni, and M. I. Abdel Aziz, 'Contribution of externally bonded FRP to shear capacity of RC flexural members', Journal of Composites for Construction, vol. 2, no. 4, pp. 195-202, 1998, doi: 10.1061/(ASCE)1090-0268(1998)2:4(195).
View Article
[6] A. Mofidi and O. Chaallal, 'Tests and Design Provisions for Reinforced-Concrete Beams Strengthened in Shear Using FRP Sheets and Strips', International Journal of Concrete Structures and Materials, vol. 8, no. 2, Art. no. 2, Jun. 2014, doi: 10.1007/s40069-013-0060-1.
View Article
[7] T. C. Triantafillou, 'Shear strengthening of reinforced concrete beams using epoxy bonded FRP composites', ACI Structural Journal, vol. 95, no. 2, pp. 107-115, 1998.
View Article
[8] S. Matthys and T. Triantafillou, 'Shear and Torsion Strengthening with Externally Bonded FRP Reinforcement', pp. 203-212, Apr. 2012, doi: 10.1061/40596(264)22.
View Article
[9] Z. Zhang, C. T. Hsu, and J. Moren, 'Shear strengthening of reinforced concrete deep beams using carbon fiber reinforced polymer laminates', Journal of Composites for Construction, vol. 8, no. 5, pp. 403-414, 2004, doi: 10.1061/(ASCE)1090-0268(2004)8:5(403).
View Article
[10] ACI Committee 440, 'Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures (440.2R-17)', American Concrete Institute, Farmington Hills MI USA, 2017.
View Article
[11] A. Belarbi, S. Bae, A. Ayoub, D. Kuchma, A. Mirmiran, and A. Okeil, Design of FRP Systems for Strengthening Concrete Girders in Shear, vol. 678. Washington, DC: Transportation Research Board, 2011.
[12] S. Matthys, 'Structural behavior and design of concrete members strengthened with externally bonded FRP reinforcement', dissertation, Ghent University, 2000.
[13] V. Colotti and G. Spadea, 'Shear Strength of RC Beams Strengthened with Bonded Steel or FRP Plates', Journal of Structural Engineering, vol. 127, no. 4, pp. 367-373, Apr. 2001, doi: 10.1061/(ASCE)0733-9445(2001)127:4(367).
View Article
[14] C. Pellegrino and C. Modena, 'Fiber Reinforced Polymer Shear Strengthening of Reinforced Concrete Beams with Transverse Steel Reinforcement', Journal of Composites for Construction, vol. 6, no. 2, pp. 104-111, May 2002, doi: 10.1061/(ASCE)1090-0268(2002)6:2(104).
View Article
[15] M. Nehdi, H. El Chabib, and A. A. Saïd, 'Proposed Shear Design Equations for FRP-Reinforced Concrete Beams Based on Genetic Algorithms Approach', Journal of Materials in Civil Engineering, vol. 19, no. 12, pp. 1033-1042, Dec. 2007, doi: 10.1061/(ASCE)0899-1561(2007)19:12(1033).
View Article
[16] M. Nehdi and H. Nikopour, 'Genetic algorithm model for shear capacity of RC beams reinforced with externally bonded FRP', Materials and Structures, vol. 44, no. 7, pp. 1249-1258, Aug. 2011, doi: 10.1617/s11527-010-9697-2.
View Article
[17] I. F. Kara, 'Prediction of shear strength of FRP-reinforced concrete beams without stirrups based on genetic programming', Advances in Engineering Software, vol. 42, no. 6, pp. 295-304, Jun. 2011, doi: 10.1016/j.advengsoft.2011.02.002.
View Article
[18] G. Hosseini, 'Capacity Prediction of RC Beams Strengthened with FRP by Artificial Neural Networks Based on Genetic Algorithm', Journal of Soft Computing in Civil Engineering, vol. 1, no. 1, pp. 93-98, Jul. 2017, doi: 10.22115/scce.2017.48392.
[19] M. Nikoo, B. Aminnejad, and A. Lork, 'Predicting Shear Strength in FRP-Reinforced Concrete Beams Using Bat Algorithm-Based Artificial Neural Network', Advanced Materials in Science and Engineering, vol. 2021, p. e5899356, Dec. 2021, doi: 10.1155/2021/5899356.
View Article
[20] M. Gasser, O. Mahmoud, T. Elsayed, and A. Deifalla, "Reliable machine learning for the shear strength of beams strengthened using externally bonded FRP jackets," Frontiers in Materials, vol. 10, 2023.
View Article
[21] T. Hu, H. Zhang, and J. Zhou, 'Prediction of the Debonding Failure of Beams Strengthened with FRP through Machine Learning Models', Buildings, vol. 13, no. 3, Art. no. 3, Mar. 2023, doi: 10.3390/buildings13030608.
View Article
[22] A. Taghipour Anvari, S. Babanajad, and A. H. Gandomi, 'Data-Driven Prediction Models for Total Shear Strength of Reinforced Concrete Beams with Fiber Reinforced Polymers Using an Evolutionary Machine Learning Approach', Engineering Structures, vol. 276, p. 115292, Feb. 2023, doi: 10.1016/j.engstruct.2022.115292.
View Article
[23] M. Shahnewaz and M. S. Alam, 'Genetic algorithm for predicting shear strength of steel fiber reinforced concrete beam with parameter identification and sensitivity analysis', Journal of Building Engineering, vol. 29, p. 101205, May 2020, doi: 10.1016/j.jobe.2020.101205.
View Article
[24] Y. Zhou, J. Zhang, W. Li, B. Hu, and X. Huang, 'Reliability-based design analysis of FRP shear strengthened reinforced concrete beams considering different FRP configurations', Compos. Struct., vol. 237, p. 111957, Apr. 2020, doi: 10.1016/j.compstruct.2020.111957.
View Article
[25] A. Belarbi, S.-W. Bae, and A. Brancaccio, 'Behavior of full-scale RC T-beams strengthened in shear with externally bonded FRP sheets', Construction and Building Materials, vol. 32, pp. 27-40, Jul. 2012, doi: 10.1016/j.conbuildmat.2010.11.102.
View Article
[26] A. Bousselham and O. Chaallal, 'Shear Strengthening Reinforced Concrete Beams with Fiber-Reinforced Polymer: Assessment of Influencing Parameters and Required Research', Structures Journal, vol. 101, no. 2, pp. 219-227, Mar. 2004, doi: 10.14359/13019.
View Article
[27] ACI Committee 318, 'Building Code Requirements for Structural Concrete and Commentary (ACI 318-19)', American Concrete Institute, Farmington Hills MI USA, 2019.
[28] M.P. Collins, "Evaluation of shear design procedures for concrete structures," Report prepared for the CSA technical committee on reinforced concrete design, 2001.
[29] 'Design and Construction of Building Components with Fiber-Reinforced Polymer', Canadian Standards Association, Rexdale, Ontario, Canada, 2002.
[30] 'Design and Construction of Building Components with Fiber-Reinforced Polymer', Canadian Standards Association, Rexdale, Ontario, Canada, 2012.
[1] J. F. Chen and J. G. Teng, 'Shear capacity of FRP-strengthened RC beams: FRP debonding', Construction and Building Materials, vol. 17, no. 1, pp. 27-41, Feb. 2003, doi: 10.1016/S0950-0618(02)00091-0. View Article
[2] A. Khalifa and A. Nanni, 'Rehabilitation of rectangular simply supported RC beams with shear deficiencies using CFRP composites', Construction and Building Materials, vol. 16, no. 3, pp. 135-146, Apr. 2002, doi: 10.1016/S0950-0618(02)00002-8. View Article
[3] J.L.T. Lima and J.A.O. Barros, "Design Models for Shear Strengthening of Reinforced Concrete Beams with Externally Bonded FRP Composites: A Statistical vs Reliability Approach," presented at the 8th International Symposium on Fiber-Reinforced Polymer Reinforcement for Concrete Structures (FRPRCS-8), University of Patras, Patras, Greece, July 16-18, 2007.
[4] T. C. Triantafillou and C. P. Antonopoulos, 'Design of concrete flexural members strengthened in shear with FRP', Journal of Composites for Construction, vol. 4, no. 4, pp. 198-205, 2000, doi: 10.1061/(ASCE)1090-0268(2000)4:4(198). View Article
[5] A. Khalifa, W. J. Gold, A. Nanni, and M. I. Abdel Aziz, 'Contribution of externally bonded FRP to shear capacity of RC flexural members', Journal of Composites for Construction, vol. 2, no. 4, pp. 195-202, 1998, doi: 10.1061/(ASCE)1090-0268(1998)2:4(195). View Article
[6] A. Mofidi and O. Chaallal, 'Tests and Design Provisions for Reinforced-Concrete Beams Strengthened in Shear Using FRP Sheets and Strips', International Journal of Concrete Structures and Materials, vol. 8, no. 2, Art. no. 2, Jun. 2014, doi: 10.1007/s40069-013-0060-1. View Article
[7] T. C. Triantafillou, 'Shear strengthening of reinforced concrete beams using epoxy bonded FRP composites', ACI Structural Journal, vol. 95, no. 2, pp. 107-115, 1998. View Article
[8] S. Matthys and T. Triantafillou, 'Shear and Torsion Strengthening with Externally Bonded FRP Reinforcement', pp. 203-212, Apr. 2012, doi: 10.1061/40596(264)22. View Article
[9] Z. Zhang, C. T. Hsu, and J. Moren, 'Shear strengthening of reinforced concrete deep beams using carbon fiber reinforced polymer laminates', Journal of Composites for Construction, vol. 8, no. 5, pp. 403-414, 2004, doi: 10.1061/(ASCE)1090-0268(2004)8:5(403). View Article
[10] ACI Committee 440, 'Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures (440.2R-17)', American Concrete Institute, Farmington Hills MI USA, 2017. View Article
[11] A. Belarbi, S. Bae, A. Ayoub, D. Kuchma, A. Mirmiran, and A. Okeil, Design of FRP Systems for Strengthening Concrete Girders in Shear, vol. 678. Washington, DC: Transportation Research Board, 2011.
[12] S. Matthys, 'Structural behavior and design of concrete members strengthened with externally bonded FRP reinforcement', dissertation, Ghent University, 2000.
[13] V. Colotti and G. Spadea, 'Shear Strength of RC Beams Strengthened with Bonded Steel or FRP Plates', Journal of Structural Engineering, vol. 127, no. 4, pp. 367-373, Apr. 2001, doi: 10.1061/(ASCE)0733-9445(2001)127:4(367). View Article
[14] C. Pellegrino and C. Modena, 'Fiber Reinforced Polymer Shear Strengthening of Reinforced Concrete Beams with Transverse Steel Reinforcement', Journal of Composites for Construction, vol. 6, no. 2, pp. 104-111, May 2002, doi: 10.1061/(ASCE)1090-0268(2002)6:2(104). View Article
[15] M. Nehdi, H. El Chabib, and A. A. Saïd, 'Proposed Shear Design Equations for FRP-Reinforced Concrete Beams Based on Genetic Algorithms Approach', Journal of Materials in Civil Engineering, vol. 19, no. 12, pp. 1033-1042, Dec. 2007, doi: 10.1061/(ASCE)0899-1561(2007)19:12(1033). View Article
[16] M. Nehdi and H. Nikopour, 'Genetic algorithm model for shear capacity of RC beams reinforced with externally bonded FRP', Materials and Structures, vol. 44, no. 7, pp. 1249-1258, Aug. 2011, doi: 10.1617/s11527-010-9697-2. View Article
[17] I. F. Kara, 'Prediction of shear strength of FRP-reinforced concrete beams without stirrups based on genetic programming', Advances in Engineering Software, vol. 42, no. 6, pp. 295-304, Jun. 2011, doi: 10.1016/j.advengsoft.2011.02.002. View Article
[18] G. Hosseini, 'Capacity Prediction of RC Beams Strengthened with FRP by Artificial Neural Networks Based on Genetic Algorithm', Journal of Soft Computing in Civil Engineering, vol. 1, no. 1, pp. 93-98, Jul. 2017, doi: 10.22115/scce.2017.48392.
[19] M. Nikoo, B. Aminnejad, and A. Lork, 'Predicting Shear Strength in FRP-Reinforced Concrete Beams Using Bat Algorithm-Based Artificial Neural Network', Advanced Materials in Science and Engineering, vol. 2021, p. e5899356, Dec. 2021, doi: 10.1155/2021/5899356. View Article
[20] M. Gasser, O. Mahmoud, T. Elsayed, and A. Deifalla, "Reliable machine learning for the shear strength of beams strengthened using externally bonded FRP jackets," Frontiers in Materials, vol. 10, 2023. View Article
[21] T. Hu, H. Zhang, and J. Zhou, 'Prediction of the Debonding Failure of Beams Strengthened with FRP through Machine Learning Models', Buildings, vol. 13, no. 3, Art. no. 3, Mar. 2023, doi: 10.3390/buildings13030608. View Article
[22] A. Taghipour Anvari, S. Babanajad, and A. H. Gandomi, 'Data-Driven Prediction Models for Total Shear Strength of Reinforced Concrete Beams with Fiber Reinforced Polymers Using an Evolutionary Machine Learning Approach', Engineering Structures, vol. 276, p. 115292, Feb. 2023, doi: 10.1016/j.engstruct.2022.115292. View Article
[23] M. Shahnewaz and M. S. Alam, 'Genetic algorithm for predicting shear strength of steel fiber reinforced concrete beam with parameter identification and sensitivity analysis', Journal of Building Engineering, vol. 29, p. 101205, May 2020, doi: 10.1016/j.jobe.2020.101205. View Article
[24] Y. Zhou, J. Zhang, W. Li, B. Hu, and X. Huang, 'Reliability-based design analysis of FRP shear strengthened reinforced concrete beams considering different FRP configurations', Compos. Struct., vol. 237, p. 111957, Apr. 2020, doi: 10.1016/j.compstruct.2020.111957. View Article
[25] A. Belarbi, S.-W. Bae, and A. Brancaccio, 'Behavior of full-scale RC T-beams strengthened in shear with externally bonded FRP sheets', Construction and Building Materials, vol. 32, pp. 27-40, Jul. 2012, doi: 10.1016/j.conbuildmat.2010.11.102. View Article
[26] A. Bousselham and O. Chaallal, 'Shear Strengthening Reinforced Concrete Beams with Fiber-Reinforced Polymer: Assessment of Influencing Parameters and Required Research', Structures Journal, vol. 101, no. 2, pp. 219-227, Mar. 2004, doi: 10.14359/13019. View Article
[27] ACI Committee 318, 'Building Code Requirements for Structural Concrete and Commentary (ACI 318-19)', American Concrete Institute, Farmington Hills MI USA, 2019.
[28] M.P. Collins, "Evaluation of shear design procedures for concrete structures," Report prepared for the CSA technical committee on reinforced concrete design, 2001.
[29] 'Design and Construction of Building Components with Fiber-Reinforced Polymer', Canadian Standards Association, Rexdale, Ontario, Canada, 2002.
[30] 'Design and Construction of Building Components with Fiber-Reinforced Polymer', Canadian Standards Association, Rexdale, Ontario, Canada, 2012.

