International Journal of Civil Infrastructure (IJCI)

ISSN: 2563-8084

1. Introduction

Bayesian network is a graphical representation of probabilistic models that show causal and effect relations between the variables and deals with uncertainties of a domain [1], [2]. It follows the concept of the probability theory, by which a certain domain is defined with a set of random variables of possible occurrences. The visual illustration of the network represents the conditional dependencies among variables for a given problem of this domain [2], [3], and shows the effect of any two conditionally independent variables on each other through intermediary variables that separate them [3]. The proposed mathematical equation used in BN algorithms is expressed in Eq. (1).

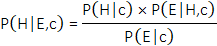
In Eq. (1), H, E, and c represent the hypothesis, evidence, and background context, respectively. The term P(H|E,c) denotes the posterior probability of the hypothesis after considering the effect of the evidence E on the context c, while P(H|c) represents the prior probability of H with respect to c alone. Conversely, P(E|H,c) signifies the likelihood of having the evidence in the case of the hypothesis and the context both true. The last term, P(E|c), can be considered as a normalizing or scaling factor, as it is independent of H [4]. The posterior probability distribution of BN is obtained by multiplying the likelihood “L”, which is defined by Eq. (2), with the prior probability and then normalizing.

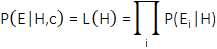
The Bayesian network consists of two main models, namely qualitative and quantitative [5]. For the qualitative models, BN correlates and finds the relationship among the variables through a causal structure learning approach [6]. Then, a direct acyclic graph (DAG) is generated to represent the variables of interest and the casual dependencies through the nodes and directed links connecting the nodes, respectively, as shown in Figure 1. In this aspect, the arrow links are directed from the parent node to its child node. As the network adopts an acyclic approach, the possibility of ending up at the same starting node is non-existent [7]. On the other hand, the quantitative models mainly concern the local probability distribution for specifying the probabilistic relationships by which the dependencies are quantified. This is performed by conditional probability tables (CPT) that classify nodes with their parents [5].

Bayesian networks have been implemented in a wide range of real-world applications, owing to their ease in the estimation of certain variables, treatment of uncertainties, and decision analysis with quick responses to the user [2]. The major applications that extensively utilize BN are risk management, quality management, financial analysis, medicine applications and diagnosis, psychological applications, and various engineering applications [2], [8]. Despite the capability of experimenting with both continuous and discrete variables, many Bayesian network algorithms only deal with the latter. As such, all continuous variables are discretized and then classified into different categories (states), such as high, medium, and low [7].

The probabilistic inference of the network is based on four steps, initial probability distribution, reasoning from cause to effect, combined influence of variables, and reasoning from the effect to the cause [7]. Further, BN learning algorithms are highly dependent on the type of infused data. In the event of using data without a hypothesis constraining the relationships between the variables, the unsupervised learning algorithms are employed. Otherwise, the supervised learning algorithms such as Naïve Bayes and Markov Blanket can be used for the inference. Naïve Bayes is considered one of the most effective learning algorithms for supervised machine learning, as it is based on the independencies between the predictors [7], [9]. On the other hand, the Markov Blanket algorithm is usually used for high-dimensional models where too many variables affect the target node [10].

This study provides the civil engineering community a new method of engaging AI techniques in civil engineering applications, in particular, to predict the mechanical properties of sustainable self-consolidated concrete by which a large amount of cement was replaced with different supplementary cementitious materials. The prediction performance of the probability-based network is assessed by comparing it with that of a typical ANN that is used to perform the prediction. It is anticipated that the probability approach can lead to a more in-depth understanding of the interaction between the concrete ingredients and their effect on the mechanical properties of the hardened concrete.

2. Related Work

Artificial Intelligence (AI) has been implemented in various engineering disciplines. The focus of employing such a technique in civil engineering is narrowed to applications where high accuracy is of interest while also saving time and resources. The implementation of the Bayesian Network in civil engineering applications has mainly focused on structural health monitoring systems.

Arangio et al. [11] combined a neural network system along with the probability logic approach of a Bayesian network. The developed system was used to identify and locate structural damage for a suspension bridge. In the study, a two-step strategy was proposed. Firstly, various neural networks were trained through inputting structural responses of a healthy structure. Then, the responses of an unhealthy structure were presented. Furthermore, the trained neural networks were integrated with the Bayesian network to optimize and improve the network’s capabilities. The new approach led to an increase of 20% in locating the occurred damage and 16% for damage quantification.

Chen et al. [12] proposed an integrated model between support vector regression (SVR) and Bayesian evidence framework (BEF) for monitoring the health of a dam structure affected by crack opening displacement (COD). Their approach entailed the application of SVR to model the nonlinear relationship between the crack opening displacement and the caused influencing factors. Meanwhile, the BEF approach was applied to determine the optimal SVR modeling parameters, such as penalty coefficient, loss coefficient, and width coefficient of the radial kernel function. The establishment of this integrated system with its suitable mathematical model enabled its use in real-life situations, where the Chencun concrete dam in China was evaluated for both normal and abnormal behaviors using this novel AI technique. As such, the presented model was found to be suitable for evaluating the behavior of cracks in concrete dams efficiently.

Ramos et al. [13] introduced a new approach on the use of probability prediction theory to assess the structural integrity of a historical building. In their methodology, test data from direct testing and past literature were used to train the Bayesian network. The tests included compressive strength, sonic, and ultrasonic testing. For the first test, core samples of granite were extracted and tested for both compressive strength and modulus of elasticity. For the non-destructive latter tests, data from the literature were collected and inputted in the Bayesian network model. As the data of these non-destructive tests have different confidence levels, a new concept for the probability distribution was introduced. In this concept, a Trust Factor (TF) was introduced to scale the standard deviation of the parameters based on their confidence level. The TF was based on the judgment of many professionals in the field. As a result, a very small variation was noticed in the mean of the modulus of elasticity. Also, the trust factor concept affected the uncertainty related to each result by increasing or decreasing their standard deviation.

Marsili et. al [14] proposed a new methodology for analyzing masonry structures based on the relationship between material strength and visual analysis. A Bayesian network was proposed based on the data that accounted for quantitative information from previously tested masonry structures and data supported by engineers specialized in masonry features. The parameters included mechanical properties of bricks, dimensions, shape, wall-leaf connection, horizontal and vertical bed joint characteristics, and mortar mechanical properties. The results revealed that the mechanical properties of masonry structures can be predicted with the network as an early reliability assessment. It was concluded that more robust validation could be accomplished using further destructive testing.

3. Experimental Methodology

Concrete design mixes with their respective results were obtained from past literature [15] to serve as a dataset to train and test the BN and ANN. The experimental data were associated with self-compacting concrete that replaced cement with various industrial by-products to promote its sustainability. This study aimed to replace up to 80% of cement with different combinations of three main supplementary cementitious materials (SCM) namely, fly ash, silica fume, and ground granulated blast furnace slag (GGBS). The study outlined three distinctive phases, namely binary, ternary, and quaternary.

In the binary mixes, the effect of partial replacement of cement with one SCM was investigated. The designed concrete mixes followed the recommendations of cement replacement from past literature [16]–[20]. Accordingly, fly ash, silica fume, and GGBS replaced cement by 0-40, 0-20, and 0-80%. In the ternary phase of the experimental program, the cement content was partially replaced with a combination of two SCMs. Finally, the quaternary phase aimed to replace 80% of the cement material with the combination of the three SCMs. Basalt fibers were introduced to the mixes in four different ratios ranging from 0.25% to 1%, by binder mass. It is worth noting that, among the mixture components, the cementitious materials and basalt fiber content varied, while the other components, such as water to binder ratio, superplasticizer content, and coarse and fine aggregates, were kept constant to reduce the number of variables.

The compressive strength test was performed on water-cured samples for 3, 7, and 28 days. A total of 226 data points were used in the current prediction study.

3. 1. Bayesian Network

Bayesialab commercial software was employed to train and test the obtained data with the BN algorithm. The software allows the user to choose from a variety of discretization techniques and converts continuous data into discrete ones (e.g., high, medium, and low) to increase the prediction accuracy. Nevertheless, the accuracy of the prediction is highly dependent on the interpretation of the acquired data by classifying the domain and all influencing variables on the results [7]. Such knowledge will ease the construction of DAG for efficient training and prediction cycles. In addition to the chosen network structure and available discretization methods, the inference of BN is highly dependent on the type of learning algorithms.

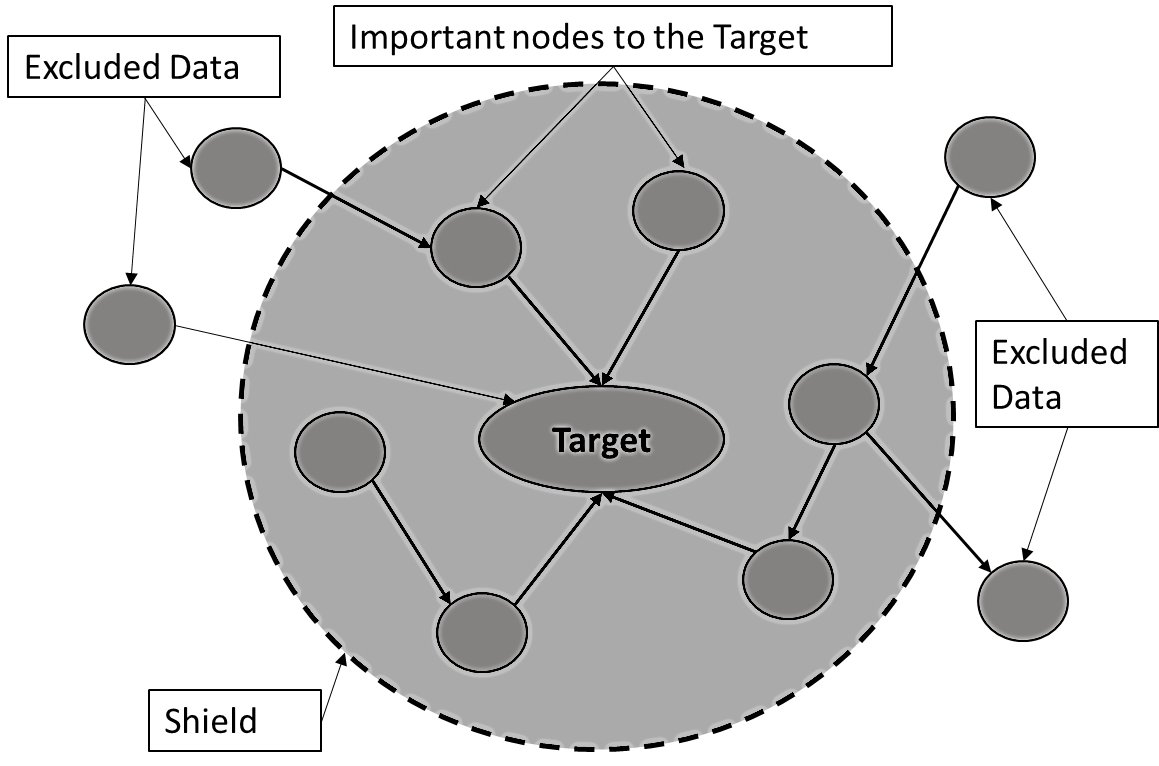
Among the various machine learning algorithms provided in Bayesialab, only two algorithms were employed in this study, namely, Naïve Bayes (NB) and Markov Blanket (MB). Naïve Bayes is considered one of the most effective learning algorithms. It is based on the independencies between the predictors, by which it assumes that each constituent has an independent effect on the results. Meanwhile, the Markov Blanket algorithm is usually used for high-dimensional models, where a large number of variables affects the target node. By using the MB algorithm, the number of parameters was reduced, as only the nodes that had hard evidence were selected to shield the target node from other nodes in the network (Figure 2).

In the current study, the developed BN combines multiple independent variables used to develop self-compacting concrete to predict the compressive strength. The independent variables that served as the network inputs included the concrete constituent and the testing age. It is worth mentioning that other impacting factors, such as water-to-binder ratio (w/b), type and quantity of coarse and fine aggregates, and type and quantity of the high range water reducer (HRWR) were fixed in the original experimental program. Thus, they were excluded from the independent variables used during the network modeling preparation. As such, the used variables were compressive strength (CS), cement (C), fly ash (F), silica fume (S), GGBS (G), basalt fibers (B), and testing age in days (D). The proposed mathematical equation for the compressive strength probabilistic inference is simplified as per Eq. (3).

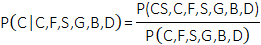
The imported data set comprised 226 data points, representing a total of 75 different mixes with 3 different testing ages and a control mix. Four different discretization methods were employed to convert the given data into discrete data. Furthermore, the data was processed by subdividing it randomly into training and testing sets to enable the network and user to validate the prediction model. The training data set used 80% of the original data, whereas the testing data set used the remaining 20%.

3. 2. Artificial Neural Network

Artificial neural network (ANN) was used to train and predict the same concrete data set employed with the Bayesian network prediction tool. ANN with a back-propagation algorithm, shown in Figure 3, was developed using MATLAB coding interface and was used to train and test the obtained data set. The developed code was for a one-hidden layer network that uses the log-sigmoid transfer function of Eq. (4).

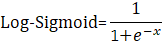
Where x is the data after being processed with initial weights.

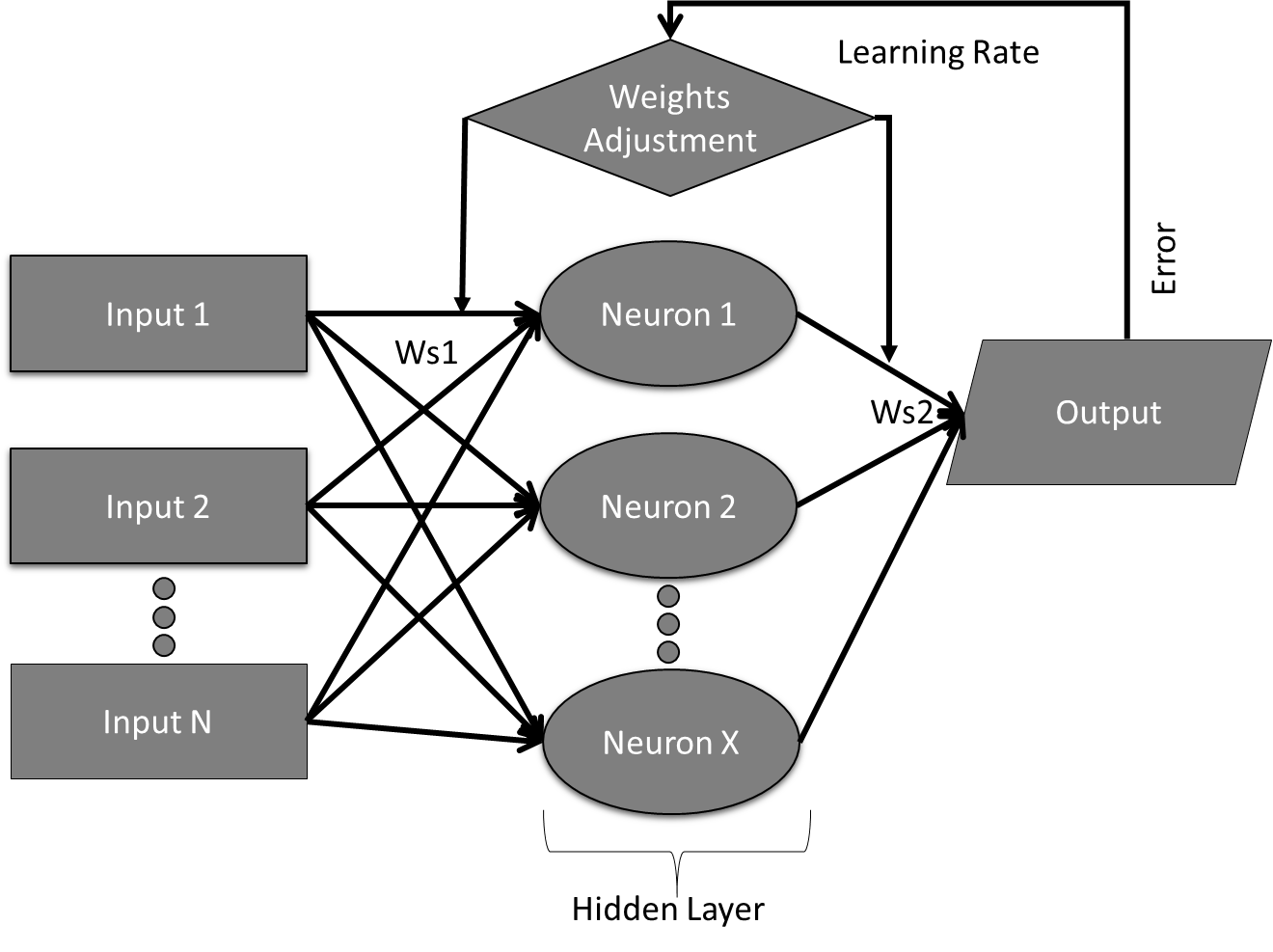
The sum of square error (SSE) with a threshold value of 0.1 was used to stop the training process. The initial weights of the input variables were chosen randomly with values between -0.5 and 0.5, while the learning rate responsible for changing the weights after each learning cycle was used in two values, 0.05 and 0.1. The exact training and testing data used in BN were employed in ANN for reliability purposes and to have accurate verification of the BN inference. Similar to the BN, the inputs used in ANN were cement (C), fly ash (F), silica fume (S), GGBS (G), basalt fibers (B), and testing age in days (D), while the output was the compressive strength. The main parameters that were changed during training were the learning rate and the number of neurons only.

To evaluate the ability of BN and ANN to predict the compressive strength of concrete used herein, the integral absolute error (IAE, %) of each technique was compared. The IAE was determined using Eq. (5).

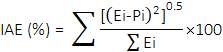
Where Ei and Pi are the experimental and predicted results.

4. Results and Discussion

4. 1. Bayesian Network

The prediction of concrete compressive strength using probabilistic inference is highly dependent on the training-testing data and the different discretization methods employed. Based on the obtained results from using Naïve Bayes or Markov Blanket algorithms, the optimum discretization method of the network was determined. Validation of the optimum results was carried out through the use of IAE (%), as it is statically more sensitive than ordinary average error [21].

Five different discretization models were utilized to maximize the network’s efficiency and minimize the IAE below 10% for acceptable performance [21]. Table 1 summarizes the IAE of the employed discretization methods. Trials with different discretization tools revealed that the k-means method with 4 segments of ‘days’ data and 3 segments of the remaining variables gave the highest correlation among all methods with an IAE of 4.26%.

This discretization tool was utilized in the Naïve Bayes algorithm to predict the concrete compressive strength. The accuracy of the BN prediction is shown in the scatter plot of Figure 4(a). The correlation coefficient, R², of the trained network was 0.71. Clearly, the predicted compressive strength results deviated from the line of equality at values below 20 MPa and above 60 MPa. Conversely, Figure 4(b) shows the predicted versus experimental compressive strength of the testing data set for the same trained network configuration. The value of R² was 0.91, indicating a more accurate prediction of the testing data.

Table 1: Different discretization tools used in the study.

Discretization Tool	IAE, %	Comments
R2-GenOpt	8.8	Default
R2-GenOpt	6.2	3 days intervals
Density Approximation	11.3	3 intervals
Density Approximation	11.3	5 intervals
K-Means	8.27	Default 3 intervals
K-Means	4.26	4 days intervals
K-Means	7.37	4 intervals all
Equal Distances	11.1	Default 3 intervals
Equal Distances	13.9	7 intervals
Equal Frequencies	9.2	Default 3 intervals
Equal Frequencies	9.9	7 intervals

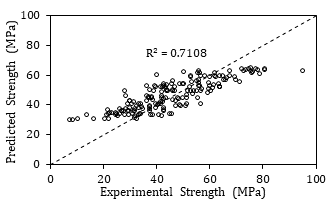
(a)
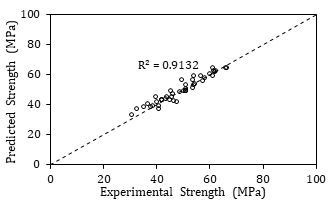
(b)

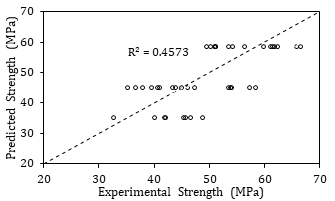
On the other hand, the Markov Blanket learning algorithm showed inconsistent results. As noted earlier, this type of algorithm uses only the highly impacting factors and shields the influence of the remaining data from the target node. In the compressive strength of concrete, the main affecting factor to the MB algorithm was the ‘days’ data set only. Thus, all other variables were excluded from the prediction of compressive strength. Consequently, the overall precisions of the learning and testing data sets were 60 and 53%, respectively. The predicted values of the compressive strength had respective values of R² and IAE of 0.46 and 13.8%, as illustrated in Figure 5. Such low precision and inaccuracy can be attributed to the limiting action of the MB algorithm to the required nodes for analysis and to restricting the variables to the testing age only.

4. 2. Artificial Neural Network

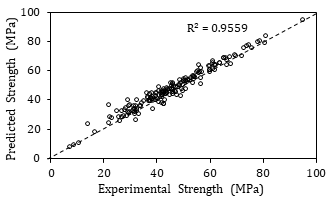
The artificial neural network training was carried out using 80% of the datasets. As described earlier, the back-propagation algorithm maintains continuous training cycles until the given SSE threshold of 0.1 is attained. The altered network parameters were the number of neurons in the hidden layer and the learning rate of the network. A total of 7 neurons were used for each network’s hidden layer. Each network was tested twice with two learning rates, namely 0.05 and 0.1, in a total of 14 network configurations shown in Table 2. The results from the different training models were with high accuracy and their corresponding R² was approximately 0.96, as depicted in Figure 6.

For the testing phase, the acquired weights from the trained networks were used to calculate the compressive strength for the remaining dataset, i.e. 20%. The obtained weights were multiplied by the data inputs from the testing set and then processed in the log-sigmoid transfer function to obtain the predicted compressive strength values. The network could accurately predict the concrete compressive strength with values of R² and IAE of 0.92 and 4.27%, respectively, as per Figure 7.

Table 2. Utilized ANN configurations in the study.

Architecture	Learning Rate	R2
6-15-1	0.05	0.873
6-15-1	0.1	0.85
6-18-1	0.05	0.854
6-18-1	0.1	0.868
6-20-1	0.05	0.856
6-20-1	0.1	0.859
6-22-1	0.05	0.874
6-22-1	0.1	0.854
6-25-1	0.05	0.862
6-25-1	0.1	0.876
6-28-1	0.05	0.92
6-28-1	0.1	0.861
6-30-1	0.05	0.859
6-30-1	0.1	0.86

4. 3. Bayesian Network vs. Artificial Neural Network

The correlation coefficients of Bayesian network training and testing phases by Naïve Bayes classifier were 0.71 and 0.91, respectively. Its integral absolute error was 4.26%. The prediction sensitivity and accuracy were found to be related to the discretization method used before processing the data. Additionally, the use of different discretization tools within the same model gave more accurate results. In contrast, outcomes of the ANN for training and testing phases were in high agreement with the experimental results with R² of 0.95 and 0.92, respectively, and an integral absolute error of 4.27%. The accuracy of the ANN can be attributed to the absence of a data discretization method before processing, as the learning algorithm of ANN depends on continuous cycles that adjust the difference between the experimental and predicted results. This is carried out through the distribution of the error between the two values among all the initial weights in the network and maintaining the process until the required level of accuracy is attained.

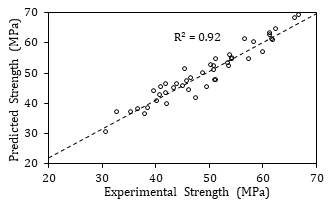
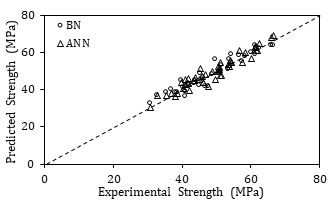
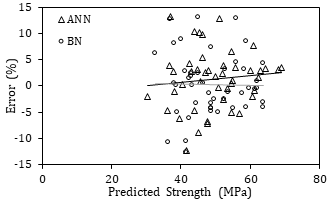
Figure 8(a) shows the compressive strength results obtained from experimental testing and those predicted by BN and ANN. It is clear that both models converge close to the 45°-line, indicating a high level of accuracy in predicting the compressive strength using both techniques. In addition, to evaluate the performance of the developed algorithms, the error between the experimental and predicted strength is plotted in Figure 8(b). The range of error generally varied between -10 and +10%, with only 6 out of the 226 data points (2.6%) falling outside this range. The trend lines associated with the ANN and BN prediction data points are also plotted. The respective slopes of the two networks were 0.061 and 0.013, indicating that the Bayesian network structure renders a slightly more accurate and precise prediction of the compressive strength.

5. Conclusions

This study uses probability-based algorithms to predict the compressive strength of concrete. Discretization methods used in the training phase of BN are highly impactful on the acquired results. The Naïve Bayes algorithm used in BN was found to be superior to Markov Blanket with IAE and R² of 4.26% and 0.91, respectively. The discretization method that was used in the Naïve Bayes algorithm to attain a high level of inference was the K-mean model discretization of 4 intervals of the ‘days’ dataset and 3 intervals for the remaining ones. Moreover, the Markov Blanket algorithm failed to predict the behavior of the compressive strength with its sole dependence on the ‘days’ parameter. The ANN model predicted the compressive strength with similar precision to that of the BN. Nevertheless, the accuracy of the BN was slightly superior to that of the ANN model. Ultimately, the compressive strength of self-compacting concrete made with different types and quantities of additives could be accurately predicted using the probabilistic inference approach through Bayesian networks.

(a)
(b)

Acknowledgments

The authors gratefully acknowledge the financial support of UAE University under grant number 31N322.

References