International Journal of Civil Infrastructure (IJCI)

ISSN: 2563-8084

1. Introduction

Liquid storage tanks are subjected to horizontal and vertical ground accelerations during earthquakes. The damages of petroleum storage tanks were reported due to earthquakes of 1933 Long Beach, 1952 Kern County, 1964 Alaska, 1971 San Fernando, 1979 Imperial Valley, 1983 Coalinga, 1992 Landers, 1994 Northridge, and 1995 Kobe [1]. The American Lifelines Alliance (ALA) [2] reported the failure modes occurred due to steel storage tanks. These failure modes are shell buckling mode, roof miscellaneous steel damage, anchorage failure, tank support system failure, foundation failure, hydrodynamic pressure failure, connecting pipe failure, and manhole failure. This study is interested in the shell buckling mode of the liquid-filled cylindrical tanks subjected to the horizontal earthquake accelerations. Based on previous studies in the literature, there are two questions that still need answers: first, How geometric imperfection can affect the seismic buckling capacity of the cylindrical steel tanks?; second, what are the interaction effects of diameter-to-thickness (D/t) and height-to-diameter (H/D) ratios on seismic local buckling strength of the steel cylindrical tanks? Therefore, the aim of this study is twofold: first, to investigate the effect of geometric imperfection on the seismic buckling strength of the cylindrical steel tanks; second, to evaluate the interaction effects of H/D and D/t ratios on the seismic buckling strengths of liquid-filled steel cylindrical tanks.

2. Literature review

In terms of the seismic behavior of the cylindrical tanks, Housner [3] reported that the hydrodynamic behaviors between water and the storage tanks which are subjected to horizontal accelerations can be distinguished into two kinds. First, impulsive mass, a mass of water is rigidly attached to the tank at the proper height. Second, convective mass, the horizontal acceleration from the tank excites a mass of water into oscillations. The impulsive and convective components should be separated to characterize the hydrodynamic response of tank–liquid systems excited horizontally [3].

Previous research was conducted to investigate the seismic local buckling of unstiffened steel cylindrical tanks using experimental study and finite element method (FEM). The buckling of tall steel cylindrical wine storage tanks was investigated using a shaking table to generate the characteristics of the 1980 Livermore earthquake [4]. Housner and Haroun [5] conducted the force vibration tests to study the dynamic response of full-scale liquid-filled steel cylindrical tanks. Seismic buckling strengths of different sizes of cylindrical steel tanks under earthquake loads were studied using FEM [6-9]. Virella [6] used a commercial finite element program ABAQUS to study dynamic buckling of the anchored steel tanks with the height-to-diameter ratio (H/D) less than 1.0, finding that the seismic buckling occurred at peak ground acceleration (PGA) between 0.25g to 0.35g. Djermane [7] evaluated the PGA values that caused the instability state of the steel cylindrical tanks using FEM. Sobhan [10] used nonlinear static pushover to investigate the buckling behavior of the anchored steel tanks, finding that bi-directional excitation obtained from static pushover analysis is similar to that obtained from dynamic buckling analysis. Sezen et al. [11] used ANSYS computer program to study liquefied gas-structure interaction and a simplified model of three tanks in Turkey that experienced an earthquake on August 17, 1999; they reported that shear and bending moments are overestimated if the fluid is modeled as a single rigid mass.

3. Finite Element Models

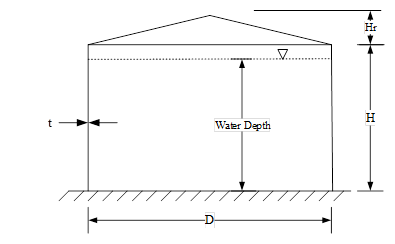
Five different geometric configurations of the cylindrical tanks are analyzed with height-to-diameter (H/D) ratios of 0.43, 0.67, 1.00, 1.46, and 2.41 and the diameter-to-thickness (D/t) ratios of 910, 1013, 1216, 1612, and 2130 to investigate the buckling behaviors of various sizes of the cylindrical tanks. The geometries of the cylindrical tanks are illustrated in Table 1 and Fig. 1.

The material for all cylindrical storage tanks is steel with a modulus of elasticity, E = 200 GPa, Poisson’s ratio, ν = 0.3, and the mass density, ρ = 7,850 kg/m3. Bilinear isotropic hardening of the steel is included with the yield stress of 345 MPa and the tangent modulus of 13.79 GPa. The liquid-filled inside the cylindrical tanks is water with the bulk modulus of 2,068.4 MPa, and the mass density of 1,000 kg/m3.

(a) (b)

Table 1. Geometries of the cylindrical tanks.

Model	H (m)	D (m)	t (mm)	Hr (m)	H/D	D/t
A	6.1	9.1	10.0	0.853	0.67	910
B	18.3	7.6	7.5	0.713	2.41	1013
C	15.2	15.2	12.5	1.425	1.00	1216
D	20.0	13.7	8.5	1.284	1.46	1612
E	9.1	21.3	10.0	2.000	0.43	2130

ANSYS computer program was used to carry all computations. SHELL181 element was used to be the element for the cylindrical steel tanks. SOLID186 element was used to be the element for water-filled inside the cylindrical tanks. SHELL181 is a four-node element with six degrees of freedom at each node (translation in x, y, and z directions, and rotation about x, y, and z axes). SOLID186 is a higher-order 3-D 20-node having three degrees of freedom per node solid element that exhibits quadratic displacement behavior [12]. The elements of SHELL181 for models A, B, C, D, and E were modeled with 4174, 5513, 8838, 7941, and 7198 elements, respectively. The elements of SOLID186 for models A, B, C, D, and E were modeled with 850, 941, 1180, 1021, and 978 elements, respectively.

4. Modal Analysis

The natural frequencies and mode shapes are the parameters that are used to find mass and stiffness coefficients for Rayleigh damping method in the transient analysis. The equation of motion for an undamped system vibrating freely is expressed in matrix notation as in Eq.1.

(1)

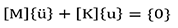
Where [M] is structural mass matrix, [K] is structural stiffness matrix, is nodal acceleration vector, and {u} is nodal displacement vector.

For a linear system, free vibration will be harmonic of the form in Eq. 2.

(2)

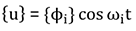
Where {ϕ_i} is eigenvector representing the mode shape of the i ^th natural frequency, ω_i is i ^th natural circular frequency in term of radians per unit time, and t is time.

The equation becomes:

(3)

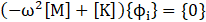
Eq. 3 is satisfied if the quantity of (-ω² [M]+[K]) or {ϕ_i} is equal to zero. However, the condition that the eigenvector is zero, {ϕ_i}=0, is trivial; therefore, this condition is not of interest. The condition of interest is Eq. 4.

(4)

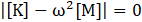
The finite element simulation may solve up to n values of ω² and {ϕ_i} to satisfy Eq. 3 where n is the number of degrees of freedoms (DOFs). In the modal analysis, the output is the natural frequencies (f) instead of the natural circular frequencies (ω) which are represented as in Eq. 5.

(5)

where f_i is i^th natural frequency in terms of cycles per unit time.

The natural frequencies of the cylindrical tanks filled with water up to 90% are represented in Table 2.

4. 1. Dumpling Ratios

Rayleigh Damping is a procedure of classical damping, which is used in the ANSYS computer program. For simplicity and numerical efficiency, the damping is assumed as Rayleigh mass proportional damping as Eq. 6 and Eq. 7.

(6)

(7)

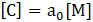
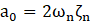
Where a₀ is mass coefficient, and ζ_n is critical damping ratio.

For the steel structure, the critical damping ratio is generally between 2% and 3% [7]. In this study, the value of 2% is adopted. This mass coefficient (a₀) is to be input into the transient analysis to indicate the damping ratio of the structure. The mass coefficients of each model are represented in Table. 2.

Table 2. First natural frequencies and mass coefficients

Model	First Natural Frequency (Hz)	Mass Coefficient (a0)
A	4.259	1.070
B	1.993	0.501
C	2.293	0.576
D	1.824	0.458
E	2.070	0.520

5. Nonlinear Seismic Analysis

The transient dynamic analysis is the technique for the response of a structure subjected to a time-dependent loading. Inertia and damping effects are considered for the transient dynamic analysis. The damping ratio of 2% is adopted in this study. The equation of motion, Eq.8, is solved by the transient structure simulation in ANSYS.

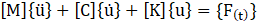
Where [M] is the mass matrix, [C] is damping matrix, [K] is stiffness matrix, is nodal acceleration vector, is nodal velocity vector, {u} is nodal displacement, {F_(t)} is load vector, and t is time.

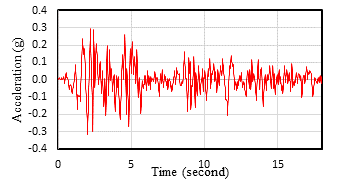
Earthquake loads in El Centro during May 18, 1940, are used in this study. Numerical values of these earthquakes are in the unit of g, the acceleration due to gravity is presented in Fig. 2. Since the PGA is 0.319g at time = 2.02 s, the accelerogram from 0 s to 8 s is used in this study to reduce CPU time-consuming.

5. 1. Perfect Geometric Tanks

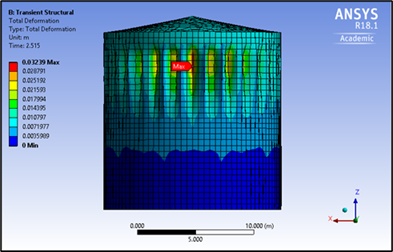
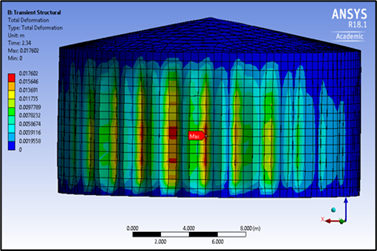
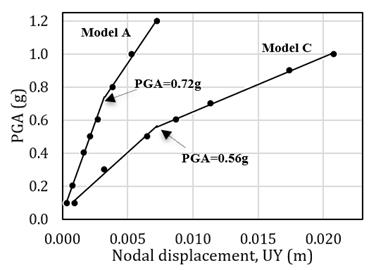
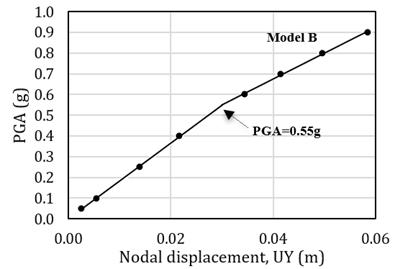
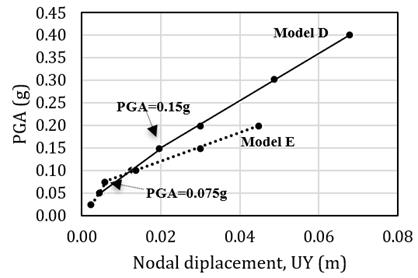
Budiansky and Roth criterion [13] was used to generate a pseudo-equilibrium path in this study. Buckling instability occurs when a small increase in the pulse intensity causes a strong increase rate of deflection. Therefore, different analyses of the structure for several loads (PGAs) must be constructed. The node which gave the maximum displacement of each model was used to find the pseudo-equilibrium path. For example, node 2638 has maximum displacement when PGA is 0.7g as illustrated in Fig. 3, and node 1725 has maximum displacement when PGA = 0.1g as illustrated in Fig. 4. Fig. 5 illustrates the pseudo-equilibrium paths and the dynamic buckling values of models A, and C. The dynamic buckling values of models A, and C are 0.72g, and 0.56g, respectively. Fig. 6 illustrates the pseudo-equilibrium paths and the dynamic buckling values of model B. The dynamic buckling value of model B is 0.55g. Fig. 7 illustrates the pseudo-equilibrium paths and the dynamic buckling values of models D and E. The dynamic buckling values of models D and E are 0.15g and 0.075g, respectively.

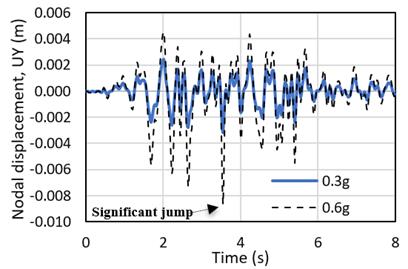
Transient response in terms of nodal displacement with an increase in PGA was also observed in this study. Fig. 8 shows the significant jump in the nodal displacement of model C which indicates that the structure is unstable for PGA = 0.6g.

5. 2. Imperfect Geometric Tanks

Imperfections of the cylindrical steel tanks are included in this study in terms of geometry imperfection to investigate the responses of the initial imperfection cylindrical steel tanks to the seismic loading. According to EC3 [14], if the construction is considered an excellent quality, Eq. 9 can be used to indicate the imperfection amplitude.

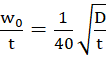
Where w₀ is the imperfection amplitude, t is the thickness of the tank, and D is the diameter of the tank.

The dynamic buckling values of the tanks decrease in the range between 5% to 33% when the initial imperfect geometries are considered. Therefore, the imperfection in geometry significantly affects the seismic buckling capacity of the cylindrical steel tank. The pseudo-equilibrium paths of initial imperfect geometric tanks are represented as in Fig. 9, 10, and 11. Fig. 12 presents the transient response curve which shows the significant jump of model D. The effects of initial imperfect geometry on the dynamic buckling capacities of the cylindrical steel tanks filled with water up to 90% height are represented in Table 3.

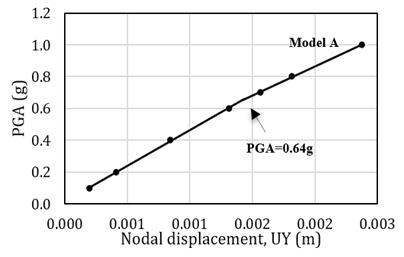
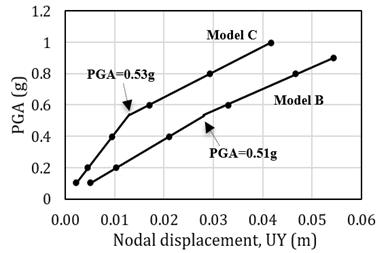
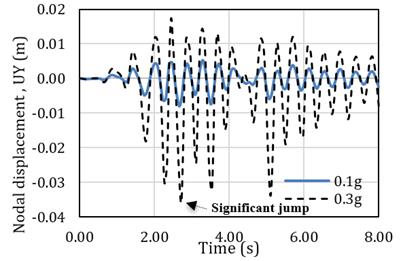
Table 3. Seismic buckling capacity

Model	H/D	D/t	Dynamic Buckling Capacity, PGA (g)
			Perfect Geometry	Initial Imperfect Geometry
A	0.67	910	0.72	0.64
B	2.41	1013	0.55	0.51
C	1.00	1216	0.56	0.53
D	1.46	1612	0.15	0.13
E	0.43	2130	0.075	0.05

5. Estimated Design Equations

Nonlinear regression analysis was adopted in this study to estimate the interaction effects of H/D and D/t ratios on the dynamic buckling capacities of the tanks for both perfect and initial imperfect geometry cases. The design equation for the geometrically perfect tanks can be estimated as Eq. 10. Design equation for the initial geometrically imperfect tanks can be estimated as Eq. 11.

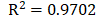
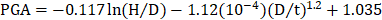
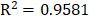
From Eqs. 10 and 11, the D/t ratio has a significant negative effect on the dynamic buckling capacity. If the D/t ratio increases, the dynamic buckling capacity will significantly decrease. An increase in the H/D ratio also shows a negative effect on dynamic buckling capacity; however, its effect is less significant than the D/t ratio.

5. Conclusion

This paper deals with the seismic buckling of steel tanks with fixed support subjected to the horizontal component of a real earthquake. The interaction effects of D/t and H/D ratios on the dynamic buckling are investigated, and estimated design equations are proposed. Results show that the D/t ratio is an important parametric factor of the seismic buckling strength of the liquid-filled cylindrical tank. The dynamic buckling capacity of the tank decreases significantly when the D/t ratio increases. An increase in the H/D ratio also seems to have a negative effect on the seismic buckling strength; however, its effect is less significant compared to the D/t ratio. Another factor that can reduce the seismic buckling strength is geometric imperfection. This study found that initial geometric imperfection significantly reduces the seismic buckling capacity.

References