International Journal of Civil Infrastructure (IJCI)

ISSN: 2563-8084

1. Introduction

The performance of the construction sector is critical in both developed and developing countries. This sector contributes to the gross domestic product and economic development of any country [1-3]. As a result, increasing construction productivity attracts more investment, boosts industry competitiveness, and creates job opportunities [4]. The construction sector is labour-intensive, with labour expenses accounting for 30-60% of the overall project expenditures [5-6]. Therefore, boosting labour productivity might improve the performance of building projects. However, the construction industry is confronted with several problems, including diminishing productivity growth [7].

Productivity is not used to estimate the cost of resources; rather, it quantifies the relationship between the resources utilized and the product produced [8-10]. In the construction industry, productivity is usually described as the ratio of an amount of output (e.g., money, product, or service) to a unit of resource input (e.g., labour, machines, materials, and money) [11]. Productivity may be quantified at three levels: industry/sector, project, and activity/process. The project productivity level is preferred since it assists construction businesses in identifying areas for improvement [12].

Quantifying and identifying the interdependencies among significant elements is required for modelling construction labour productivity. The current method of predicting productivity rates is based on an estimator's opinion, published productivity data, or previous project data. Personal bias and staff turnover impact the accuracy of depending on estimators' views. The reported productivity figures do not reflect a contractor's performance, but rather the industry's average productivity rates [13]. Past project data generally yields the most accurate and trustworthy estimate [1]. As a result, proper modelling of construction labour productivity allows avoiding the subjectivity and irrelevance of the old technique. These models capture the variance in productivity with regard to the influencing input parameters, resulting in successful construction project planning and scheduling [14-15].

2. Related Work

Artificial intelligence is deemed to be an effective technique for forecasting construction labor productivity. Heravi and Eslamdoost [16] employed a back propagation neural network (BPNN) model to predict labour productivity. When early stopping and Bayesian regularization were compared, Bayesian regularization outperformed early stopping. A sensitivity analysis was also performed to assess the impact of each input element on the prediction performance of the models. El-Gohary et al. [1] applied neural networks to estimate construction labour productivity. To benchmark construction labour productivity, many activation and transfer functions, as well as a wide variety of influencing factors, were used. When compared to standard approaches in the literature, the suggested model produced more accurate findings.

Golnaraghi et al. [8] compared the results of BPNN, general regression neural network (GRNN), radial base function neural network (RBFNN), and adaptive neuro-fuzzy inference system (ANFIS) to evaluate labour productivity. According to the results, BPNN outperformed other approaches for predicting labor productivity. Mlybari [17] estimated labour productivity using GRNN, artificial neural networks (ANN), support vector machine (SVM), and multiple additive regression trees (MART). According to the findings, the GRNN model outperformed the other approaches for forecasting labour productivity in concrete pouring and finishing as well as steel fixing.

Mohammed Abdelkader et al. [18] compared an ensemble of machine learning models for the sake of estimating loss of productivity as a result of change orders. In the developed model, the loss of productivity was quantified with regards to type of work, its impact, number of change orders, their frequency, average size of change orders and change order hours. The utilized machine learning models encompassed radial basis neural network, generalized regression neural network, cascade forward neural network, Elman neural network, back propagation neural network, multiple linear regression and hybrid particle swarm optimization-liner regression. It was evinced that radial basis neural network surpassed other machine learning models attaining mean absolute percentage error, mean absolute error and root mean square error of 2.44%, 0.014 and 0.027, respectively.

Agrawal and Halder [19] studied factors that influence construction labour productivity. By adopting relative importance index, the levels of importance of the studied factors were explored. Results demonstrated that appointing competent project labour, payments on time and skilled labour were appended as the most implicating indicators on labour’s productivity. Alrefaie et al. [20] deployed polynomial regression to forecast labour productivity of reinforcement rebar. In their model, a set of explanatory variables was studied such as rainfall distribution, solar radiation, dry bulb temperature, wind speed and relative humidity. Results illustrated that weather conditions managed to influence labour’s productivity by 43%.

Hai and Van Tam [21] built a regression-based model to analyse labour’s productivity of construction workers. They tackled factors pertaining to work time, motivation, working safety, working conditions, natural environment, etc. It was anticipated that factors in relation with construction workers are highly influential on labour productivity. Dixit [22] investigated the factors influencing on-site construction productivity drawing on multiple regression and statistical analysis. It was revealed that change in scope, revision in drawings and response to change orders highly impact construction productivity.

3. Model Development

The framework of the developed model for forecasting the labour productivity of formwork assembly is presented in this section. The framework, as illustrated in Figure 1. The first step is to define the factors affecting labour productivity in high rise buildings. The present research study explores the implementation of eight types of data-driven machine learning models, namely ANFIS-GA, ANFIS-PSO, GRNN [23-24], BP-ANN [25-26], ENN [27-28], RT [29-30], SVM [31-32] and GPR [33-34]. The validation process is carried out hinging upon the performance metrics of MAPE, MAE, RMSE, RAE and RRSE. In the ANFIS-GA and ANFIS-PSO, genetic algorithm and particle swarm optimization algorithms are used to estimate the parameters of the membership function in the ANFIS model. Using the input and target data, the fuzzy inference system is built. The ANFIS model output is calculated, and error objective functions are minimized [35]. Some machine learning models may over perform with regards to some performance metrics. However, they may under perform with respect to others. Hence, average ranking algorithm is exploited to establish a consolidated ranking of the data-driven models [36-37]. Eventually, a correlation matrix is constructed to look into the dependencies between the input and output variables.

4. Performance Metrics

As discussed previously, the developed model accommodates the five performance evaluation metrics of MAPE, MAE, RMSE, RAE and RRSE that are described in Eq. 1, Eq. 2, Eq. 3, Eq. 4 and Eq. 5, respectively [38-41].

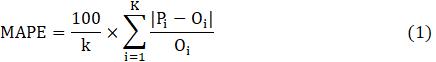
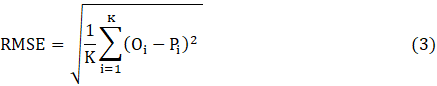
Where K is number of available observations in the dataset. O_i and P_i are the actual and predicted labour productivities, respectively. It should be highlighted that lower values of MAPE, MAE, RMSE, RAE and RRSE indicate more accurate intelligent data-driven model.

5. Numerical Example

Over eighteen months, data on labour productivity was collected from two high-rise buildings in Montreal, Canada [42]. The first structure was built of concrete and had a flat slab construction system. It had 17 floors and a surface area of 68,000 m2, and it took three years to build. The second structure employed the same structural system as the first. These projects include a total of 221 data points for formwork activity. The data includes project, crew, and weather-related parameters. Data related to job type and procedure, as well as floor level, are classed as project data, whereas gang size and labor percentage belong to crew data. The factors utilized in the weather category include temperature, humidity, precipitation, and wind speed.

The aforementioned factors must be taken into account since they affect daily work productivity. Table 1 depicts additional statistical parameters for the nine variables. It should be noted that the work type includes three forms of formwork: slabs (1), walls (2), and columns (3). Furthermore, the work approach incorporates built-in place (1) and flying forms (2). The number of floors is referred to as the floor level. The gang size in the crew category refers to the number of people in a crew. In addition, the labour percentage is the ratio of labour size to gang size. Temperature, humidity, and wind speed are measured in Celsius (Co), percentage (%), and kilometres per hour, respectively. Furthermore, precipitation can be classified as no precipitation (0), light rain (1), snow (2), or rain (3).

The effectiveness of the developed data-driven models for forecasting formwork labour productivity is investigated in this study. To anticipate worker productivity in two high-rise buildings in Montreal, Canada, the traditional BP-ANN model is used as the benchmark model. The dataset is divided into two parts: 80 percent for training and 20 percent for testing.

Table 1. Statistical parameters of input and output factors.

Variable	Min	Max	Mean	Standard deviation
Work type (C1)	1	3	1.43	0.51
Work method (C2)	1	2	1.44	0.50
Floor level (C3)	1	17	11.38	3.75
Gang size (C4)	8	24	16.03	5.07
Labour percentage (C5)	29	47	35.49	3.79
Temperature(C6)	-26	25	4.08	12.03
Humidity(C7)	18	97	66.34	15.67
Precipitation (C8)	0	3	0.28	0.60
Wind speed (C9)	3	43	15.42	8.46
Productivity (Y1)	0.82	2.53	1.57	0.35

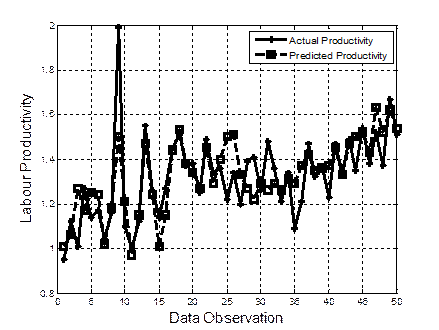
A sample of 50 data observations of the actual and predicted labour productivity using RT, BP-ANN and ANFIS-PSO are presented in Figures 2, 3 and 4, respectively. It can be noticed that RT managed to simulate the actual labour productivity accurately producing very close predicted values to the actual ones. As for BP-ANN, it managed to yield acceptable level of accuracies. However, it still underperformed in some data observations. With regards to ANFIS-PSO, it failed to predict the actual labour productivity resulting very far predicted values from the actual values.

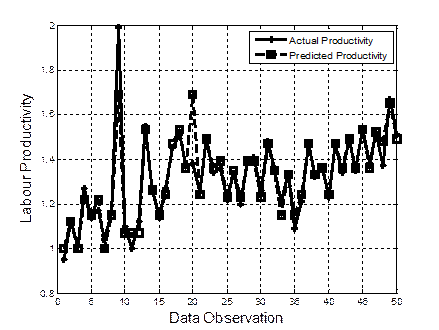
The error histograms with 25 bins in RT, BP-ANN and ANFIS-PSO models are depicted in Figures 5, 6 and 7, respectively. It can observed that RT managed to induce very close values to zero error in most of the instances.

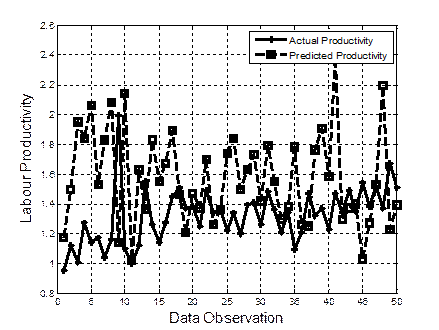
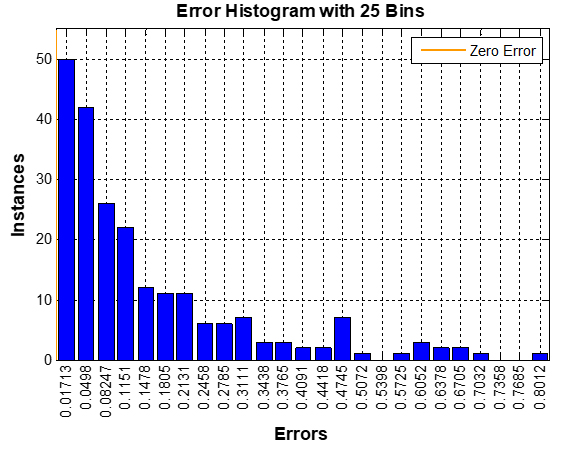
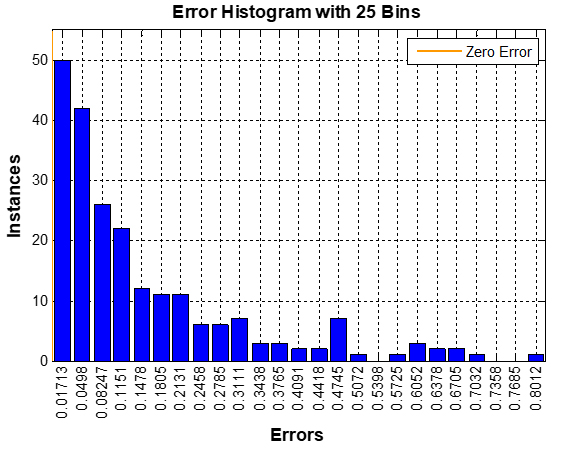
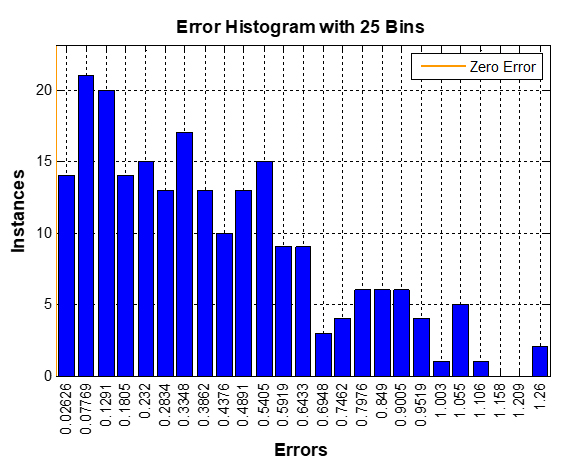
Table 2 reports a comparison between simulated and actual labour productivity estimates. GRNN model accomplished high prediction performance, whereas it provided MAPE, MAE, RMSE, RAE and RRSE of 7.21%, 0.1, 0.22, 0.35 and 0.63, respectively. GRNN also achieved very promising results attaining MAPE, MAE, RMSE, RAE and RRSE of 8.98%, 0.13, 0.19, 0.45 and 0.54, respectively. On the contrary, ANFIS-PSO yielded the highest prediction errors such that its values of MAPE, MAE, RMSE, RAE and RRSE are 26.26%, 0.4, 0.5, 1.4 and 1.4, respectively. ENN obtained acceptable prediction performance with MAPE, MAE, RMSE, RAE and RRSE are 10.33%, 0.15, 0.22, 0.52 and 0.62, respectively.

Table 2: Comparative analysis of the data-driven models for predicting labour productivity.

Prediction model	MAPE	MAE	RMSE	RAE	RRSE
ANFIS-GA	23.47%	0.35	0.44	1.22	1.25
ANFIS-PSO	26.26%	0.40	0.50	1.40	1.40
GRNN	8.98%	0.13	0.19	0.45	0.54
BP-ANN	10.38%	0.15	0.22	0.53	0.63
ENN	10.33%	0.15	0.22	0.52	0.62
RT	7.21%	0.10	0.22	0.35	0.63
SVM	20.31%	0.31	0.39	1.07	1.10
GPR	10.03%	0.149	0.21	0.52	0.59

The results of the average ranking algorithm are recorded in Table 3. As can be seen, GRNN outranked the remainder of the data-driven models whereas it accomplished mean and standard deviation of 0.8 and 1.4, respectively. RT was ranked in the second place followed by GPR in the third place. On the other hand, ANFIS-PSO and ANFIS-PSO were ranked in the seventh and eight places, respectively. Analytical comparisons also illustrated that GRNN provided the most stable and robust performance with least standard deviation. However, RT and GPR experienced explicit variations across the multiple performance indicators.

Table 3: Final rankings of data-driven models.

Prediction model	Mean ranking	Standard deviation of rankings	Final ranking
ANFIS-GA	7	0	7
ANFIS-PSO	8	0	8
GRNN	1.8	0.40	1
BP-ANN	4.6	0.49	5
ENN	3.2	0.40	4
RT	2.6	1.96	2
SVM	6	0	6
GPR	2.8	1.17	3

Table 5 reports the correlation between the design input explanatory variables and labour productivity. It can be interpreted that the highest level of correlation existed between gang size and temperature, gang size and wind speed, and labour productivity and temperature. It is also shown that temperature and work method exhibit the highest influence on labour productivity. On the other hand, humidity and labour percentage have the least correlation with labour productivity. In this regard, the correlation values of work method, temperature, humidity and labour percentage with labour productivity are -0.353, 0.589, -0.053 and 0.09, respectively.

6. Conclusion

This study presented eight intelligent data-driven models for forecasting labour productivity in high rise buildings. To assess the effectiveness of the suggested models, historical data from two high-rise structures were collected. Eighty percent of the data was utilized to train the models, while the remaining twenty percent was used to test and validate the models. As input parameters for the models, nine factors related to the project, crew, and weather conditions were chosen. Performance analysis evinced that GRNN provided the lowest prediction error (MAPE 8.98%, MAE 0.13, RMSE 0.19, RAE 0.45 and RRSE 0.54). Nevertheless, ANFIS-PSO obtained the lowest prediction accuracies (MAPE 26.26%, MAE 0.4, RMSE 0.5, RAE 1.4 and RRSE 1.4). In this regard, GRNN performed better than BP-ANN, ENN, SVM, GPR, ANFIS-GA and ANFIS-PSO by 13.97%, 13.28%, 54.8%, 10.94%, 60.27% and 60.98%, respectively. It was also inferred that GRNN produced the most stable ranking over the five investigated performance indicators. As for GPR and RT, their rankings were highly variable with the performance indicators. It was also found that RT accomplished the second ranking based on the average ranking algorithm while ANFIS-GA and ANFIS-PSO were the lowest ranked intelligent data-driven models. The correlation analysis manifested that work method and temperature are highly correlated with formwork labour productivity while humidity and labour productivity are less influential on the labour productivity. As a result, the GRNN can be stand as an improved decision-making platform for predicting formwork labor productivity in high rise buildings.

Table 4: Final rankings of data-driven models.

	C1	C2	C3	C4	C5	C6	C7	C8	C9	Y1
C1	1	-0.761	-0.052	-0.175	-0.135	-0.122	-0.110	-0.037	0.065	-0.353
C2		1	0.225	-0.036	0.177	0.078	0.176	-0.057	0.030	0.328
C3			1	-0.352	0.142	0.358	0.048	-0.288	0.235	0.301
C4				1	-0.310	0.390	-0.167	0.065	-0.415	0.183
C5					1	-0.120	0.219	-0.063	0.051	-0.053
C6						1	0.151	-0.093	-0.122	0.589
C7							1	0.338	0.026	0.090
C8								1	0.076	-0.175
C9									1	-0.202
Y1										1

References