1. Introduction

Many bridges constructed during the period of rapid economic growth in the 1960s and 1970s have aged, while the shortage of skilled inspectors has become a serious issue for infrastructure maintenance. Vibration-based non-destructive testing methods are widely used on site to detect structural damage and deterioration. Dynamic bridge characteristics, including natural frequencies and damping ratios are estimated using several methods: ambient vibration measurements using microtremors [1], impact excitation [2], and forced vibration tests employing shakers [3].

   These testing methods are selected depending on the purpose and site conditions. Among these methods, impact excitation tests are most commonly used in Japan for inspecting railway bridge piers to identify dynamic properties such as natural frequencies and damping ratios. However, these results depend on the skill of the inspector. In the case of road bridges, partial traffic restrictions are often required for excitation tests. Therefore, the use of quantitative excitation with shakers and long-term measurements using ambient vibrations are also considered promising. Fukagawa et al. [4] analytically demonstrated that a dual-sine excitation using a shaker can reproduce quasi-static loading conditions under dynamic vibration for the purpose of estimating bridge stiffness. However, this method requires direct displacement measurement. In contrast, this study aims to identify dynamic characteristics based on acceleration responses, which are more practical for on-site monitoring by measuring from the bridge deck. Furthermore, to the choice of excitation and measurement methods, Kato et al. [5] reported that vibration characteristics like natural frequencies and damping ratios are affected by external factors such as temperature and excitation level.

   In addition, to simplify excitation testing, methods using vehicles running over the bridge as moving excitation sources have also been proposed. Yang et al. [6] theoretically presented a method for estimating the natural frequencies of bridges by analysing the frequency spectrum of vehicle acceleration responses. Oshima et al. [7] attempted to identify bridge natural frequencies using a large vehicle equipped with a shaker and accelerometers mounted on a two-wheeled test rig.

However, although the identification of bridge natural frequencies from moving vehicles has been theoretically demonstrated to be feasible, challenges remain in distinguishing bridge responses from the vibration components of the vehicle itself when applied to actual bridges.

Therefore, in this study, quantitative excitation tests and long-term measurements were conducted on a real bridge to investigate the effects of excitation method, temperature, and excitation level on its dynamic characteristics. Previous studies have mainly conducted statistical analyses on the effects of external factors, such as temperature, on the dynamic characteristics of structures. In contrast, this study is distinguished by its focus on long-term and quantitative investigation of these variations on an actual bridge.

Furthermore, as a first step to toward identifying bridge natural frequencies using moving vehicles, excitation tests were carried out on an actual bridge using a dolly equipped with a shaker, and the bridge’s natural frequencies were identified by analysing the acceleration responses measured on the dolly. This approach, which integrates excitation and measurement in a mobile system, aims to simplify conventional shaker-based excitation tests and achieve more efficient and accurate monitoring of bridge dynamic characteristics.

2. Methodology for Bridge Vibration Characterization under Varying Excitation Conditions

2. 1. Target Bridge

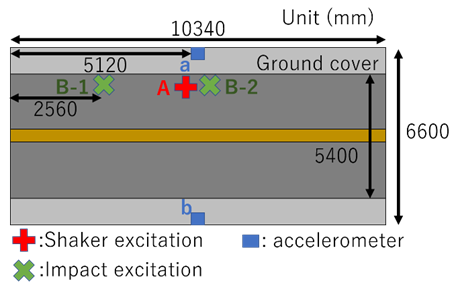
The target bridge is a short-span concrete girder bridge with a length of 10 m. Figure 1 shows the bridge, and Figure 2 provides a top view of the bridge layout, which is used in the subsequent analysis.

2. 2. Experiment Condition

Three types of excitation tests were conducted: a shaker test, an impact excitation test, and a constant microtremor test.

Although the shaker test allows for controlled excitation, the shaker itself is heavy and makes in-service testing of bridges impossible. In this study, a shaker weighing about 70 kg was used. In the impact excitation test, the bridge was struck using a hammer weighing 4 kg and the natural frequency was obtained from the response. Although this method is simple, it is not possible to test bridges while they are in service and the test results also depend on the skill of the inspector. The constant microtremor test measures vibrations from different sources, including wind, ambient ground motion and traffic. The advantage of this test is that no special excitation is required, however the excitation force remains unknown.

Table 1 summarizes the objectives and excitation methods used in each experimental series. In the first experimental series, the objective was to compare three excitation methods: shaker excitation (at position A in Figure 2), impact excitation (at position B-1 and B-2 in Figure 2), and ambient vibration measurement using constant microtremors. Accelerometers were placed at positions a and b as shown in Figure 2. The second series investigated amplitude dependency of vibration characteristics using the shaker placed at the same position as in the first series, with the excitation level was controlled over ten steps. The accelerometer was placed at position a in Figure 2. The third test examined temperature dependency of vibration characteristics by measuring constant microtremors over an extended period using sensors at positions a and b in Figure 2.





2. 3. Analysis Method

Natural frequencies were identified using the peak of both the Power Spectral Density (PSD) and the Random Decrement (RD) method, whereas damping ratios were determined using the half power method and RD method.

The RD method reproduces a free-damping waveform by overlapping and averaging several responses over time and assumes that noise is random and has a mean of zero [8]. Curve fitting is then applied to the generated waveform to identify natural frequencies and damping ratios.

The half-power method identifies damping ratios using the frequencies where the power spectral density drops to 1/√2 of its peak value. Since the target modes in this study were well-defined and the vibration data included random noise, such as constant microtremors, the half-power and RD methods were selected.

3. Influence of Excitation Conditions on Identified Vibration Characteristics

3. 1. Target Bridge

a) Excitation methods

The shaker test involved six 2-minute upward sweeps from 5 Hz to 60 Hz. In the impact excitation test, the bridge was struck 10 times at the center and at 1/4 of the span, where the data was analyzed by connecting the data obtained 10 seconds after each excitation. For the constant microtremor test, data collected over approximately one hour was analyzed. Figure 3 and Figure 4 show the shaker test and the impact excitation test, respectively.

b) Results

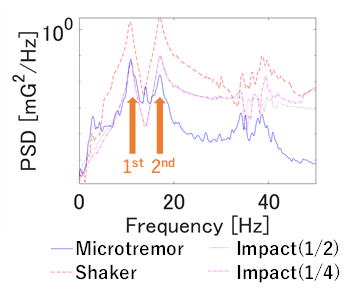
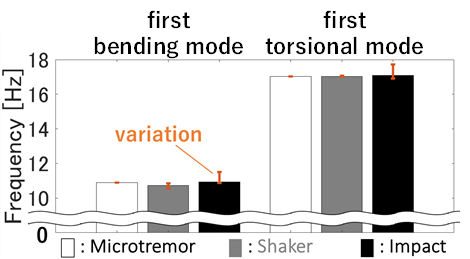
From the frequency-PSD diagram for each test, as shown in Figure 5, two dominant vibration modes were clearly identified; the first bending mode at 10.7 Hz and the first torsional mode at 17.0 Hz. The following sections focus on these two dominant modes, as they were clearly and consistently observed across all test methods.

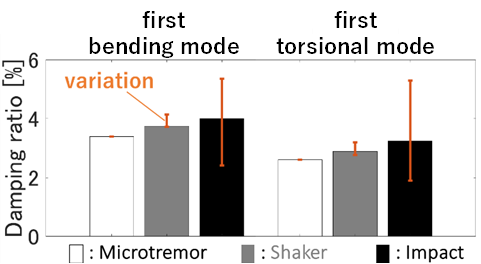
Figure 6 and Figure 7 show the identified natural frequencies and damping ratios for each test method, as well as the variation in identified natural frequencies and damping ratios across multiple tests. The peak PSD and half power method were used for analysis. In general, damping ratios exhibited greater variation than natural frequencies. However, as shown in Figure 7, the variations in the identified natural frequencies and damping ratios were smaller for the shaker excitation test.

Table1. The objectives and methods of the excitation tests.

	Objective	Excitation methods
No. 1	Comparison of excitation methods	Shaker Impact excitation Constant microtremor
No. 2	Study of amplitude dependence	Shaker
No. 3	Study of temperature dependence	Constant microtremor (long time measurement)













3.2. Different excitation levels

a) Excitation conditions

The shaker was set to perform an upward sweep from 5 Hz to 25 Hz in 30-second cycles, where 10 different excitation levels were applied.

b) Results

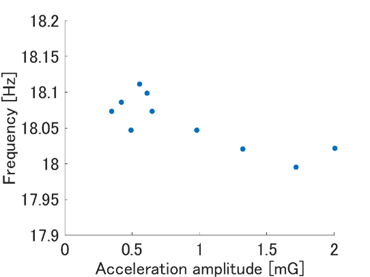
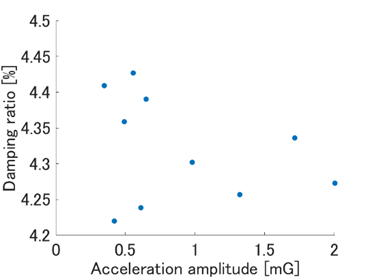
As shown in Figure 8, the natural frequency of the first torsional mode decreased with increasing acceleration amplitude. However, Figure 9, shows no clear correlation between the acceleration amplitude and the identified damping ratio. These observations, that frequency and damping do not exhibit the expected negative correlation under steady-state vibration, suggest that another factor is at play.

One possible explanation is that the bearing condition affected the results. At high excitation levels, slight movement in the bearings may have caused the natural frequency to fluctuate, whereas at low levels the bearings remained stationary.

3.3. Different temperature conditions

a) Data conditions

A total of 59 data sets were used for each period during constant microtremor measurements, namely day (13:00 to 15:00) and night (1:00 to 3:00). The key difference between the two periods was in the acceleration amplitude where the night data ranged between approximately 0.02 mG and 0.04 mG, while the day data ranged between approximately 0.06 mG and 0.17 mG.

b) Results

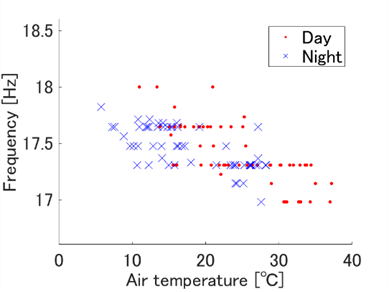
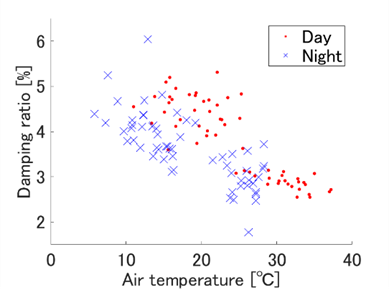
As shown in Figure 10 and Figure 11, both identified natural frequencies and damping ratio values for the first torsional mode tend to decrease as temperature increases. The natural frequency of the first bending mode also showed a similar trend. This is likely because the physical property of the bridge material, namely concrete, is affected by temperature changes.

A linear regression analysis was performed on all 118 identified natural frequency data sets with respect to temperatures. As a result, an increase of 1℃ in air temperature led to a decrease of 0.021 Hz in the first bending mode and 0.024 Hz in the first torsional mode. This behaviour is due to the influence of temperature variations on the physical properties of the concrete composing the bridge.

Given that the coefficient of linear thermal expansion for concrete is approximately 1.0×10^-5/℃, the 10 m span concrete bridge investigated in this study









expands or contracts by about 0.1 mm per 1℃ change. Consequently, as the temperature increases, the span length slightly increases, resulting in a decrease in the natural frequencies.

 

4. Natural Frequency Identification Method Using a Moving Shaker Vehicle

a) Overview of test method

A novel approach to monitor bridge vibration has been explored in this study, by mounting a shaker onto a moving dolly. This method aims to overcome the operational limitations of traditional shaker-based tests, offering a potentially simpler and more efficient solution for dynamic testing. While the shaker test provides high accuracy, its practical application is constrained by its complex setup. The proposed moving vehicle-based method seeks to streamline this process by combining excitation and measurements in one single mobile setup.

Firstly, the natural frequency of the dolly itself was evaluated to understand its vibration characteristics. Next, the shaker mounted on the moving dolly was used to excite the bridge while the dolly was in motion. By comparing the results with conventional stationary tests, the study evaluates the feasibility of this mobile method and proposes a new technique for identifying the natural frequencies of a target bridge during movement.

b) Vibration characteristics of moving vehicle

An excitation test was conducted on the dolly with the shaker mounted. As shown in Figure 12, one accelerometer was placed on the shaker and six were attached to the dolly, near each of the four wheels and between the front and rear wheels. The natural frequencies of the dolly were estimated to be around 10 Hz and in the range of 16 Hz to 20 Hz, corresponding to different vibration modes of the dolly.

During preliminary analysis, it was found that sensors placed between the front and rear wheels were affected by bending deformation and thus provided unstable measurements. Therefore, sensors were confirmed by consistent phase difference and transfer function results from the wheel-mounted sensors.

4.2. Measurement conditions

Excitation was applied on the bridge via a moving the dolly. As shown in Figure 13, the shaker was mounted on the dolly and accelerometers were attached to the dolly. For the moving measurements, ropes were tied to both ends of the dolly and pulled, allowing it to traverse the bridge from one end to another, as illustrated in Figure 14 and Figure 15. The dolly moved at approximately 0.5 m/s, and the shaker was set to adjust the excitation frequencies between 10 Hz and 12 Hz for the first bending mode and between 16 Hz and 18 Hz for the first torsional mode, using a sweep period of 1 second. For comparison, excitation was also performed with a stationary dolly at the center of the bridge.

4.3. Proposed method to identify natural frequencies from moving vehicle

In the comparison test using the moving dolly, the natural frequencies of the bridge were evaluated under both stationary and moving conditions, as summarized in Table 2. The frequencies identified under stationary conditions were 11.5 Hz for the first bending mode and 17.7 Hz for the first torsional mode. Under moving conditions, the corresponding frequencies were identified as 11.6 Hz and 16.4 Hz, respectively. Accordingly, it was confirmed that natural frequencies can be identified with high accuracy even under moving conditions: less than 1% relative error for the first bending mode and approximately 7.3% for the first tortional mode compared to stationary measurements.

The 1% error observed in the first bending mode can be considered sufficiently practical for bridge maintenance and management purpose. In contrast, the 7.3% error in the first torsional mode is relatively large, indicating room for improvement in identification accuracy. At higher frequencies, the vibration period becomes shorter, resulting in a shorter resonance duration, which is likely to cause larger identification errors. As a future task, it is necessary to further improve the identification accuracy by reducing noise from the moving dolly and other sources.

Since conventional FFT analysis is generally unsuitable for identifying natural frequencies during motion, a resonance-based method was adopted. As shown in Figure 16, the moving average of acceleration data from the dolly was computed, and peaks corresponding to resonance between the dolly and the bridge were extracted. These peaks were then mapped onto the resulting scalograms obtained from the Continuous Wavelet Transform (CWT), enabling the identification of the natural frequencies of the bridge.







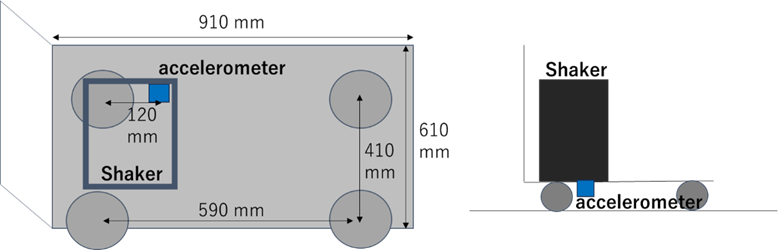
Table. 2 Identified natural frequencies of the bridge

	Parking	Moving
First bending mode	11.5 Hz	11.6 Hz
First torsional mode	17.7 Hz	16.4 Hz



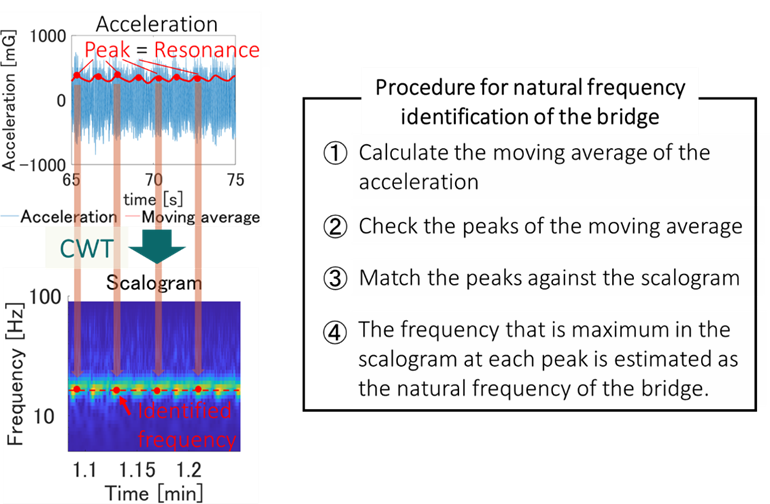
The CWT-based analysis was performed separately for each of the four test runs, and the identified natural frequencies were then averaged to obtain the final values in Table 2. This method has confirmed that the natural frequencies of this bridge can be identified using a moving vehicle, where stable frequency identification was achieved through CWT analysis of the acceleration data from the dolly.

4.4. Significance of the proposal method

This novel approach, using a shaker mounted on a moving dolly, offers a more practical and efficient bridge inspection method, by eliminating the need for fixed excitation systems and reducing operational constraints. The results indicate that despite the inherent challenges in dealing with moving measurements, analyzing the resonance between a (given) bridge and moving dolly using CWT can offer more accurate and stable identification of the natural frequencies of the given bridge. If further refined, this method could enable more accessible, cost-effective monitoring without requiring extensive infrastructure changes.

5. Conclusions

In this study, excitation measurements were conducted using different excitation methods, temperatures, and excitation levels to investigate the factors that affect bridge vibration characteristics and the applicability of a mobile shaker system.

1) Bridge natural frequencies and damping ratios were identified using multiple excitation tests. The results show greater variability in damping ratios compared to natural frequencies. However, the use of a shaker minimized fluctuations in the identified values, demonstrating its effectiveness in achieving stable vibration measurements.

2) It was found that natural frequencies decrease as the acceleration amplitude of bridge increases. This phenomenon was likely related to the movement conditions of the bridge bearings, which can shift under higher excitation levels. Moreover, both natural frequencies and damping ratios decreased with increasing temperature. This behaviour is considered to be caused by the thermal expansion and contraction of concrete associated with temperature variations.

3) A simple system for identifying the natural frequencies from a moving vehicle was examined, considering excitation methods and external disturbances. The results demonstrate the possibility of identifying the natural frequencies of a bridge from a moving vehicle, using the resonance found between the bridge and the moving vehicle with CWT. This approach is expected to serve as a promising step toward achieving faster and more efficient structural health monitoring compared with conventional shaker-based tests.

This study evaluated fluctuations in the vibration characteristics of bridges under varying excitation and environmental conditions. In addition, a new approach was proposed for identifying natural frequencies using a moving vehicle, offering a practical alternative to conventional excitation methods. The proposed method to identify the natural frequencies of a bridge using a moving vehicle offers significant advantages over conventional methods, paving the way for more accessible and cost-effective monitoring solutions.

However, this study was limited to a relatively short-span girder bridge with a span of approximately 10m. For application to longer and heavier bridges, it is necessary to examine the excitation capacity of the mobile shaker to ensure that sufficient excitation force can be provided. Furthermore, in identifying natural vibrations using moving vehicles, larger errors were observed in higher-order modes. Therefore, improvements such as adjusting the natural frequencies of the moving vehicle and reducing noise are expected to enhance the accuracy of the identification.




References

[1] Ryuji TAKESHIMA, Reem AI SEHNAWI, Akinori NAKAJIMA, Susumu NAKAMURA, Hideaki YOKOKAWA: A Study on Change of Vibration Property of Bridge Structure with RC Pier in Different Vibration Level, Journal of Japan Society of Civil Engineers, Vol. 70, No.4, pp. I_130-I_139, 2014. View Article

[2] Masaki MIYAMURA, Hideki NAITO, Satoshi NAKANO, Masuo KADO, Ichiro IWAKI, Motoyuki SUZUKI: Study on Evaluation of Structural Performance in 15-year-old PC Road Bridge after Reconstruction under Severe Chloride Environment, Journal of Japan Society of Civil Engineers, Ser. E2(Materials and Concrete Structures), 72(2), pp. 41-55, 2016. View Article

[3] Isao OKAUCHI, Toshio MIYATA, Masaaki TATSUMI Nobuyuki SASAKI: Field vibration test of a long-span cable stayed bridge by large exciters. Proceedings of Japan Society of Civil Engineers, No. 455, pp. 75-84, 1992. View Article

[4] Youzou FUKAGAWA, Hisao EMOTO: a Stiffness Estimation for Bridges with Dual Sine Forces Oscillating Method, Journal of Japan Society of Civil Engineers, Ser. A2(Applied Mechanics), Vol. 78, No. 1, pp. 23-31, 2022. View Article

[5] Masafumi KATO, Shizuo SHIMADA: Statistical Analysis on the Measured Bridge Vibration Data, Proceedings of Japan Society of Civil Engineers, No. 311, pp. 49-58, 1981. View Article

[6] Yang, Y. B., Lin, C. W. and Yau, J. D.: Extracting Bridge Frequencies from the Dynamic Response of a Passing Vehicle, Journal of Sound and Vibration, No. 272, pp.471-493, 2004. View Article

[7] Yoshinobu OSHIMA, Yoshikazu KOBAYASHI, Takashi YAMAGUCHI, Kunitomo SUGIURA: Fundamental Study of Vibration Transfer Between Bridge and Passing Vehicles, Journal of Japan Society of Civil Engineers, Ser. A1(Structural and Earthquake Engineering), 68(2), pp. 384-397, 2012. View Article

[8] Yukio TAMURA, Atsushi SASAKI, Haruo TSUKAGOSHI: Evaluation of Damping Ratios of Randomly Excited Buildings Using the Random Decrement Technique, Journal of Structural Construction Engineering, AIJ, No.4544, Dec, 1993. View Article